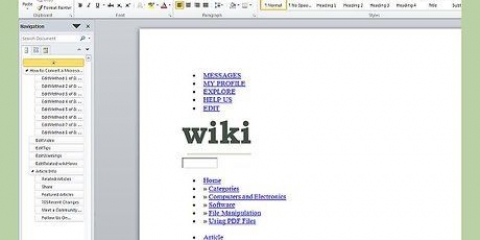
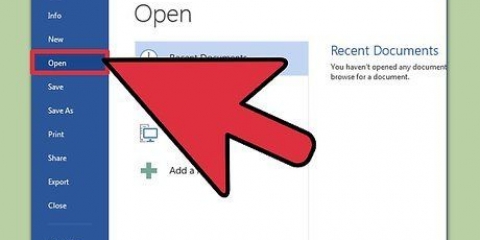
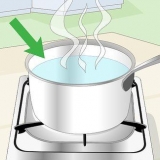
A23 = 1010 0010 0011 BEE= 1011 1110 1110 70C558= 0111 0000 1100 0101 0101 1000
Du kan også tenke på dette som tallsystemer som samtidig `bytter` til et annet tall. Heksadesimaltall`...D, E, F, 10` mens binær samtidig teller som `1101, 1110, 1111, 10000`. 

Starter med tallet helt til høyre, 7 = 7 x 10, eller 7 x 1 Lenger til venstre er 3 = 3 x 10 eller 3 x 10 Gjenta dette for alle tall, og du får 480.137 = 4x100 000 + 8x10.000 + 0x1000 + 1x100 + 3x10 + 7x1.
116 = 1 x 16 = 1 x 1 (Alle tall er i desimalform, unntatt der det er angitt.) 216 = 2 x 16 = 2 x 16 916 = 9 x 16 = 9 x 256 C = C x 16 = C x 4096
A = 10 B = 11 C = 12 (Vi bruker dette i eksemplet ovenfor.) D = 13 E = 14 F = 15
C92116 = (i desimal) (1 x1) + (2 x16) + (9 x 256) + (12 x 4096) = 1 + 32 + 2304 + 49.152. = 51.48910. Desimalversjonen vil vanligvis ha flere sifre enn den heksadesimale versjonen, fordi heksadesimale tall inneholder mer informasjon per siffer.
3AB16 = 93910 A1A116 = 4137710 500016 = 2048010 500D16 = 2049310 18A2F16 = 10091110 

Konverter heksadesimale tall til desimaltall
Innhold
Hvordan gjør du de morsomme tallene og bokstavene til noe datamaskinen din kan forstå? Konvertering fra heksadesimal til binær er veldig enkelt, og det er grunnen til at heksadesimal er inkludert i noen programmeringsspråk. Konvertering til desimal er litt vanskeligere, men når du først finner ut av det, kan du enkelt gjenta dette for et hvilket som helst tall.
Trinn
Del 1 av 3: Konvertering av heksadesimal til binær
1. Konverter et hvilket som helst heksadesimalt tegn til et 4-sifret binært tall. Heksadesimalen har kommet i bruk i utgangspunktet fordi konverteringen mellom de to er så enkel. I hovedsak er heksadesimalen ment som en måte å representere binær informasjon på en forkortet måte. Følgende tabell er alt du trenger for å utføre denne konverteringen:| heksadesimal | binær |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| en | 1010 |
| B | 1011 |
| C | 1100 |
| d | 1101 |
| E | 1110 |
| f | 1111 |

2. Prøv selv. Det er egentlig så enkelt som å endre sifferet eller tegnet til de fire ekvivalente binære sifrene. Her er noen heksede tall du kan konvertere. Velg den usynlige teksten til høyre for likhetstegnet for å sjekke svaret ditt:

3. Forstå hvorfor dette fungerer. I det binære systemet, med `base 2`, n binære sifre kan brukes til å representere 2 forskjellige tall. For eksempel: med fire binære tall du kan 2 = foreslå 16 forskjellige tall. Dette gjør konverteringen mellom de to tallsystemene spesielt enkel.
Del 2 av 3: Konvertering av heksadesimal til desimal

1. Finn ut hvordan base 10 fungerer. Du bruker desimalnotasjon hver dag uten å tenke på nøyaktig hva som skjer, men når du først lærte det, kan det hende at lærerne eller foreldrene dine har forklart det mer detaljert. En kort forklaring på hvordan vanlige tall skrives vil hjelpe deg å konvertere tallet:
- Hvert siffer i et desimaltall er på et bestemt "sted".` Hvis du går fra høyre til venstre, vil du støte på `enheter`, `tiere`, `hundrevis` og så videre. Tallet 3 betyr ganske enkelt 3 når det er i enhetene, men 30 når det er på tiere og 300 når det er i hundre.
- For å si det matematisk: `stedene` er 10, 10, 10 osv. på. Dette er grunnen til at systemet også kalles "grunntall 10" eller "desimal", etter det latinske ordet for "tiende".`

2. Skriv et desimaltall som en sum. Dette virker åpenbart, men er den samme prosessen som vi vil bruke til å konvertere et heksadesimalt tall, så det er et godt sted å starte. La oss gjøre det til 480.13710 konvertere. (Husk at abonnementet 10 forteller oss at dette er et tall med grunntall 10.):

3. Skriv plassverdiene ved siden av det heksadesimale tallet. Siden heksadesimalen har 16 som base, tilsvarer `stedsverdiene` potensene 16. For å konvertere til desimal, multipliser hver plassverdi med den tilsvarende potensen 16. Begynn denne prosessen ved å skrive potensene til 16 ved siden av sifrene i et heksadesimalt tall. Vi skal gjøre dette for det heksadesimale tallet C92116. Start til høyre med 16, øk eksponenten hver gang du flytter til venstre, til neste siffer:

4. Konverter bokstaver til desimaler. Numeriske sifre er alle like i desimal eller heksadesimal, så du trenger ikke å endre dem (f.eks., 716 = 710). Når du har å gjøre med bokstaver, bruk følgende liste for å endre dem til desimalekvivalenter:

5. Utfør beregningen. Nå som alt er skrevet i desimalform, gjør hver utregning og legg sammen resultatene. En kalkulator er nyttig for de fleste heksadesimale tall. Fortsetter med vårt tidligere eksempel, omskriver vi C921 som en desimalformel og løser for det:

6. Øv på konverteringen. Her er noen heksadesimale tall for å konvertere til desimaltall. Når du har funnet svaret, velg den usynlige teksten til høyre for likhetstegnet for å sjekke svaret:
Del 3 av 3: Forstå det grunnleggende om heksadesimal

1. Vet hvordan du bruker heksadesimal. Desimaltallsystemet har en grunntall 10, og bruker 10 forskjellige tegn for å representere tall. Heksadesimalen er base 16 tallsystem, som betyr at den bruker 16 forskjellige tegn for å representere tall.
- Teller fra 0 og oppover:
heksadesimal desimal heksadesimal desimal 0 0 10 16 1 1 11 17 2 2 12 18 3 3 1. 3 19 4 4 14 20 5 5 15 21 6 6 16 22 7 7 17 23 8 8 18 24 9 9 19 25 en 10 1A 26 B 11 1B 27 C 12 1C 28 d 1. 3 1D 29 E 14 1E 30 f 15 1F 31

2. Bruk subscript for å angi hvilket nummersystem du bruker. Hvis det ikke er klart hvilket tallsystem du bruker, bruk et desimaltegn for å angi grunntallet. For eksempel: 1710 betyr `17 med grunntall 10` (et vanlig desimaltall). 1710 = 1116, eller `11 med base 16` (heksadesimal). Du trenger ikke å gjøre dette hvis nummeret ditt inneholder en bokstav, for eksempel B eller E. Ingen vil gjøre en feil og tro at det er et desimaltall.
Tips
- Lange heksadesimale tall kan kreve en online kalkulator for å konvertere til et desimaltall. Du kan også hoppe over alt arbeidet og bruke Windows-kalkulatoren (som inkluderer en omformer), eller la en online omformer gjøre jobben for deg, selv om det er en god idé å forstå hvordan prosedyren fungerer.
- Du kan bruke `heksadesimal til desimal` konvertering for å konvertere et hvilket som helst grunntallsystem X konvertere til desimaltall. Bare bytt ut kraften til 16 med kraften til X. Prøv å lære det babylonske tallsystemet med base 60!
Artikler om emnet "Konverter heksadesimale tall til desimaltall"
Оцените, пожалуйста статью
Lignende
Populær