Måle en vinkel uten vinkelmåler

Innhold

Trinn
Tips
Nødvendigheter

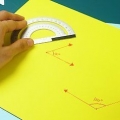
Den enkleste måten å måle en vinkel på er med a gradskive. Men hvis du ikke har en gradskive tilgjengelig, kan du bestemme størrelsen på en vinkel ved å bruke de grunnleggende geometriske prinsippene for trekanter. Du trenger en vitenskapelig kalkulator for å løse ligningene. De fleste smarttelefoner er utstyrt med det, men du kan også laste ned gratis apper eller bruke en gratis kalkulator på nettet. Beregningene du må gjøre avhenger av om du har å gjøre med en spiss vinkel (mindre enn 90 grader), stump vinkel (mer enn 90 grader men mindre enn 180), eller en `refleksvinkel` (mer enn 180 grader men mindre) . enn 360).

Trinn

Metode 1 av 3: Skarpt hjørne

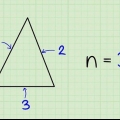
1. Tegn en vertikal linje som forbinder de to strålene i vinkelen. For å finne antall grader i en spiss vinkel, koble sammen de to strålene for å danne en trekant. Juster den korte enden av linjalen din med den nederste strålen, og tegn deretter en vertikal linje som skjærer den andre strålen ved å bruke langsiden av linjalen din.

Den vertikale linjen lager en rettvinklet trekant. Vinkelen dannet av den tilstøtende siden (den nedre radius av vinkelen) av trekanten og den motsatte siden (den vertikale linjen) er 90 grader.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 2

2. Mål lengden på den tilstøtende siden rundt den tilstøtende eller x-verdi finne. Plasser enden av linjalen din på toppunktet. Mål lengden på den tilstøtende siden fra toppunktet til punktet der den skjærer motsatt side.

Denne verdien er x-verdien i helningsligningen din, der helning = y/x. Så hvis du målte 7, vil ligningen din være "helling = y/7".

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 3

3. Vi måler lengden på den andre siden for å finne det motsatte. Juster den korte enden av linjalen din med den tilstøtende siden av trekanten. Mål lengden på den vertikale linjen fra punktet der den møter den tilstøtende siden til punktet der den møter den øvre radiusen til hjørnet (hypotenusen til trekanten din).

Dette beløpet er det motsatte eller y-verdi i helningsligningen din. Så hvis du målte 5, blir ligningen "helling = 5/7".

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 4

4. Del det motsatte med det tilstøtende (y-verdien med x-verdien) for å finne helningen til vinkelen. Skråningen er brattheten til den diagonale linjen, eller hypotenusen, til trekanten din. Når du vet dette tallet, kan du beregne gradene av den spisse vinkelen din.

Så for å fortsette eksemplet, blir ligningen `slope = 5/7` og det er 0,71428571.

Tips: Ikke rund av tallet før du konverterer dette tallet til grader – ellers blir resultatet mindre nøyaktig.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 5

5. Bruk kalkulatoren til å beregne vinkel i grader. Skriv inn helningsverdien i den vitenskapelige kalkulatoren, og trykk deretter på invers tangent (tan)-knappen. Dette vil gi deg vinkelen i grader.

For å fortsette med eksemplet gir en helning på 0,71428571 en vinkel på 35,5 grader.

Metode 2 av 3: Stump vinkel

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 6

1. Forleng den nederste radius av hjørnet i en rett linje. Merk toppunktet med et punkt, og bruk så langsiden av linjalen til å tegne en rett linje til venstre for toppunktet. Den nederste radiusen til hjørnet skal være en enkelt lang linje som strekker seg under den åpne toppradiusen til hjørnet.

Sørg for at linjen er helt rett. Hvis linjen er vinklet opp eller ned, vil det ødelegge nøyaktigheten til ligningen din.

Tips: Hvis du jobber med papir uten linjer, kan du justere kortsiden av linjalen med siden av papiret for å sikre at linjeforlengelsen er rett.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 7

2. Tegn en vertikal linje som forbinder den øverste strålen med linjen. Juster kortsiden av linjalen med den nederste strålen på et punkt der langsiden skjærer den øverste strålen. Følg langsiden for å tegne en linje rett opp fra den nedre strålen som forbinder de to.

Effektivt har du laget en liten rett vinkel ved den stumpe vinkelen du vil måle, noe som gjør den øvre radiusen til den stumpe vinkelen til hypotenusen til den rette vinkelen.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 8

3. Mål lengden på bunnlinjen fra toppunktet. Plasser linjalen din under den nederste linjen, og start ved den vertikale linjen og skaper den rette vinkelen. Mål lengden fra det skjæringspunktet til toppunktet til den opprinnelige vinkelen.

Du bestemmer helningen til vinkelen til den spisse trekanten, som du kan beregne gradene i den spisse vinkelen med. Bunnlinjen er ved siden av verdi i ligningen `helling = motsatt/tilstøtende`.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 9

4. Mål lengden på den vertikale linjen. Juster den korte enden av linjalen din med den nederste linjen i den lille spisse trekanten. Mål med linjalen til punktet der den vertikale linjen skjærer den åpne radiusen til din stumpe vinkel. Dette er lengden på den vertikale linjen.

Lengden på den vertikale linjen er motsatte verdi i ligningen `helling = motsatt/tilstøtende`. Hvis du kjenner verdiene for både motsatt og tilstøtende, kan du beregne helningen til den spisse vinkelen.

Bilde med tittelen Mål en vinkel uten vinkelmåler Trinn 10

5. Bestem helningen til den spisse vinkelen. Del motsatte verdi av ved siden av verdi for å bestemme helningen til den spisse vinkelen. Du vil bruke denne verdien til å beregne den spisse vinkelen i grader.

For eksempel vil ligningen `helling = 2/4` gi en helning på 0,5.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 11

6. Beregn gradene av den spisse vinkelen. Skriv inn skråningen i den vitenskapelige kalkulatoren, og trykk deretter på `invers brunfarge`-knappen. Verdien som vises er antall grader av den spisse vinkelen.

For å fortsette med eksemplet, hvis helningen din er 0,5, er den spisse vinkelen en vinkel på 26,565 grader.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 12

7. Trekk fra antall grader av den spisse vinkelen fra 180. En flat linje er en rett vinkel med 180 grader. Siden du har tegnet en rett linje, vil summen av den spisse vinkelen du beregnet og den stumpe vinkelen være 180 grader. Å trekke fra gradene av den spisse vinkelen fra 180 gir deg antall grader av den stumpe vinkelen din.

For å fortsette med eksemplet, hvis du har en spiss vinkel på 26.565 grader, har du en stump vinkel på 153.435 grader (180 – 26.565 = 153.435).

Metode 3 av 3: Refleksvinkel (stump vinkel > 180)

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 13

1. Bestem den minste spisse vinkelen knyttet til den stumpe vinkelen som er større enn 180 grader (heretter: Refleksvinkel). En refleksvinkel er større enn 180 grader, men mindre enn 360 grader. Dette betyr at hvis du ser på refleksvinkelen, vil du også se en spiss vinkel innenfor den.

Ved å bestemme antall grader av den spisse vinkelen, kan du beregne antall grader av refleksvinkelen. Du kan bruke den grunnleggende helningsligningen og den inverse tangentfunksjonen på den vitenskapelige kalkulatoren for å finne gradene av den spisse vinkelen.

Tips: Hvis du er forvirret fordi vinkelen er opp ned, snu papiret og ignorer refleksvinkelen til siste trinn.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 14

2. Tegn en vertikal linje som forbinder strålene i den spisse vinkelen. Juster den korte enden av linjalen med radiusen til hjørnet som er horisontalt i stedet for diagonalt. Tegn deretter en vertikal linje som krysser den horisontale radiusen til hjørnet.

Den horisontale linjen vil være den tilstøtende siden av trekanten din, og den vertikale linjen vil være motsatt side av den spisse vinkelen du vil måle.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 15

3. Mål den motsatte og den tilstøtende linjen til den spisse vinkelen. I ligningen `helling = motsatt/tilstøtende`, er det motsatte lengden på den vertikale linjen, eller motsatt side av trekanten din. Tilstøtende er lengden på den horisontale linjen, eller den tilstøtende siden av trekanten din.

Mål den horisontale linjen fra toppunktet til punktet der den skjærer den vertikale linjen. Mål den vertikale linjen fra punktet der den skjærer den horisontale linjen til punktet der den skjærer den diagonale linjen.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 16

4. Del det motsatte med det tilstøtende for å beregne helningen til den spisse vinkelen. Bruk verdiene som er funnet for lengden på de vertikale og horisontale linjene i helningsligningen din. Når du deler lengden på den vertikale linjen med lengden på den horisontale linjen, får du helningen for vinkelen.

For eksempel, hvis den horisontale linjen er 8 og den vertikale linjen er 4, blir ligningen din "helling = 4/8". Helningen på vinkelen din er da 0,5.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 17

5. Bruk kalkulatoren til å finne gradene av den spisse vinkelen. Skriv inn verdien du har for helningen til vinkelen i den vitenskapelige kalkulatoren og trykk deretter på `invers tangent` (tan)-knappen. Verdien som vises er antall grader av den mindre, spisse vinkelen.

For å fortsette med eksemplet, hvis helningen din er 0,5, vil den spisse vinkelen være 26,565 grader.

Bilde med tittelen Mål en vinkel uten en gradskive Trinn 18

6. Trekk fra antall grader av den spisse vinkelen fra 360. En sirkel har 360 grader. Siden en refleksvinkel er en vinkel større enn 180 grader, betrakt den som en del av en sirkel. Gradene av refleksvinkelen og gradene av den mindre spisse vinkelen summerer seg til 360.

For å fortsette med eksemplet, hvis den minste spisse vinkelen er 26.565 grader, er refleksvinkelen 333.435 grader.

Tips

Sørg for at den vitenskapelige kalkulatorens trigonometriske funksjoner er satt i grader, ikke radianer.
Helningen er forholdet mellom x-bevegelsen og y-bevegelsen. Måleenheten du bruker for å kvantifisere lengdene på de to linjene er irrelevant - bare pass på at du bruker samme enhet for begge linjene. Med andre ord, hvis du måler lengden på den ene linjen i centimeter, må du også måle den andre i centimeter.