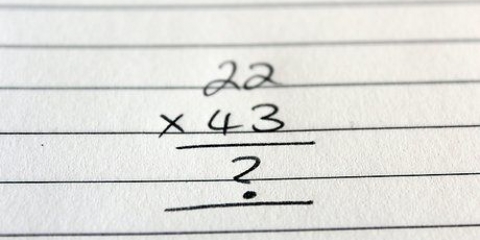11 > 1, altså 11 "passer ikke" 1. Skriv en 0 som det første sifferet i kvotienten (over det første sifferet i utbyttet). 
Få ned neste siffer i utbyttet. 11 > 10. Skriv en 0 i kvotienten. Få ned neste tall. 11 < 101. Skriv en 1 i kvotienten. 
Skriv divisoren under utbyttet. Her skriver vi dette som 11 under de tre første sifrene (101) i utbyttet. Regn ut 101 - 11 for resten, 10. Se gjennom hvordan du trekker fra binære tall hvis du ikke husker det. 
Skriv 11 under 100 og trekk fra disse tallene for å få 1. Få ned siste siffer i utbyttet og du får 11 som svar. 11 = 11, så du skriver 1 som siste siffer i kvotienten (svaret). Det er ingen rest, så oppgaven er fullført. Svaret er 00111, eller enklere, 111. 
Å dele binære tall resulterer ofte i at tall gjentas etter desimaltegnet, oftere enn de som forekommer med desimalnotasjon. Dette refereres til med den mer generelle termen "radikspunkt" som du møter i et hvilket som helst tallsystem, fordi du har "desimal tegn" kun påtruffet innenfor desimalsystemet. 

Finn komplementet til enene i det andre leddet, trekk hvert siffer fra 1. Du kan enkelt gjøre dette med binære tall ved å sette hver 1 til 0 og hver 0 til 1. I vårt eksempel er 011 lik 100. Legg til 1 til resultatet: 100 + 1 = 101. Dette kalles 2-komplementet. Vi skal nå vurdere en minussum som en tilleggssum. Essensen er at vi anser problemet som om vi legger til et negativt tall i stedet for å trekke fra et positivt tall, etter å ha fullført prosedyren. Legg resultatet til den første termen. Løs summen: 111 + 101 = 1100. Utelat det første sifferet (bær sifferet). Fjern det første sifferet fra svaret for å få det endelige resultatet. 1100 → 100. 

2s komplement av 000101 = 111010 + 1 = 111011 100011 + 111011 = 1011110 Utelat det første sifferet (bæringen) → 011110 

011110 + 111011 = 1011001 → 011001 (kvotient 1+1=10) 011001 + 111011 = 1010100 → 010100 (kvotient 10+1=11) 010100 + 111011 = 1001111 → 001111 (11+1=100) 001111 + 111011 = 1001010 → 001010 (100+1=101) 001010 + 111011 = 10000101 → 0000101 (101+1=110) 0000101 + 111011 = 1000000 → 000000 (110+1=111) 0 er mindre enn 101, så vi kan stoppe nå. Kvotienten 111 er svaret på delproblemet. Resten er det endelige resultatet av minsummen vår, i dette tilfellet 0 (ingen hvile).
Deling av binære tall
Å dele binære tall kan løses ved å bruke lang divisjon, en praktisk metode for å lære deg selv prosedyren eller skrive et enkelt dataprogram. Alternativt tilbyr komplementmetoden med gjentatt subtraksjon en tilnærming du kanskje ikke er kjent med, selv om den egentlig ikke er mye brukt i programmering. Maskinspråk bruker vanligvis en estimeringsalgoritme for større effektivitet, men disse er ikke beskrevet her.
Trinn
Metode 1 av 2: Bruke lang divisjon

1. Gå over desimal lang divisjon igjen. Hvis det er en stund siden du gjorde lang divisjon med vanlige desimaltall (grunntall 10), se gjennom basen for oppgaven 172 ÷ 4. Ellers hopper du over dette og går til neste trinn for å lære denne prosedyren for binære tall.
- Den utbytte er delt med divisor, og svaret er det kvotient.
- Sammenlign deleren med det første sifferet i utbyttet. Hvis divisor er det største tallet, fortsett å legge til sifre til utbyttet til divisor er det minste tallet. (Som et eksempel, når vi beregner 172 ÷ 4, sammenligner vi 4 og 1, finner vi at 4 > 1, og sammenlign deretter 4 med 17.)
- Skriv det første sifferet i kvotienten over det siste sifferet i utbyttet som brukes til sammenligning. Etter å ha sammenlignet 4 og 17, legger vi merke til at 4 går inn i 17 fire ganger, så vi skriver 4 som det første sifferet i kvotienten vår, over 7.
- Multipliser og trekk fra for å finne resten. Multipliser kvotienten med divisor, i dette tilfellet 4 x 4 = 16. Skriv 16 under 17, og gjør deretter 17 - 16 for resten, 1.
- Gjenta. Igjen sammenligner vi divisor 4 med neste siffer, 1, vi legger merke til at 4 > 1, og "bringe" vi flytter neste siffer i utbyttet ned for å sammenligne 4 med 12 i stedet. 4 går inn i 12 tre ganger uten rest, så vi kan skrive 3 som neste siffer i kvotienten. Svaret er 43.

2. Lag et binært langdivisjonsoppsett. Anta at vi bruker som eksempel 10101 ÷ 11. Skriv dette som lang divisjon, med 10101 som utbytte og 11 som divisor. La det være plass over for å skrive kvotienten, og skriv beregningene dine under den.

3. Sammenlign deleren med det første sifferet i utbyttet. Dette fungerer på samme måte som desimal lang divisjon, men er faktisk mye enklere i binær form. Enten kan du ikke dele tallet med divisor (0), eller så passer divisor inn én gang (1):

4. Ta nå neste tall og gjenta til du får 1. Her er de neste trinnene fra vårt eksempel:

5. Bestem resten. som i desimal lang divisjon, multipliserer vi sifferet vi nettopp fant (1) med divisoren (11), og skriver resultatet under utbyttet vårt på en linje med sifferet vi nettopp beregnet. I binær form kan vi gjøre dette raskere, fordi 1 x divisor alltid er lik divisor:

6. Fortsett til problemet er løst. Ta med neste siffer fra forhandleren til resten nedenfor for å få 100. Fordi 11 < 100 skriver du en 1 som neste siffer i kvotienten. Fortsett å løse problemet som før:

7. Legg til et radixpunkt om nødvendig. Noen ganger er ikke resultatet et heltall. Hvis du fortsatt har en rest etter å ha brukt det siste sifferet, legg til en ".0" til utbytte og en "." til kvotienten din slik at du kan få ned ett tall til og gå videre. Fortsett med dette til du oppnår ønsket nøyaktighet, og rund deretter av svaret. På papir kan du avrunde ved å utelate 0 eller, hvis det siste sifferet er en 1, trekke det fra og legge til 1 til det siste sifferet. Når du programmerer, bruk en av standard avrundingsalgoritmer for å unngå feil ved konvertering mellom binære og desimaltall.
Metode 2 av 2: Bruke komplementmetoden

1. Forstå den grunnleggende ideen. En måte å løse divisjoner på – for en hvilken som helst base – er å fortsette å trekke divisoren fra utbyttet, deretter resten, og regne ut hvor mange ganger du kan fortsette å gjøre dette før du kommer til et negativt tall. Her er et eksempel for grunntallet 10, oppgaven 26 ÷ 7:
- 26 - 7 = 19 (1 ganger trukket fra)
- 19 - 7 = 12 (2 ganger trukket fra)
- 12 - 7 = 5 (3 ganger trukket fra)
- 5 - 7 = -2. Negativt tall, så opp igjen. Svaret er 3 med en rest på 5. Merk at denne metoden ikke tar hensyn til desimaler.

2. Lær å trekke fra ved hjelp av komplementer. Selv om du enkelt kan bruke metoden ovenfor på binære tall, kan vi også bruke en mer effektiv metode, som kan spare deg for tid når du programmerer binære divisjoner. Dette kalles den binære komplementmetoden. Her er det grunnleggende, der vi beregner 111 - 011 (sørg for at begge tallene er like lange):

3. Kombiner de to konseptene ovenfor. Nå vet du hvordan subtraksjonsmetoden for å løse divisjoner fungerer, og 2-komplementmetoden for å løse summen av minuser. Du kan kombinere de to til én metode for å løse divisjonsproblemer ved å bruke trinnene nedenfor. Hvis du vil kan du prøve å finne det ut selv før du fortsetter.

4. Trekk divisor fra utbyttet ved å legge til 2-komplementet. La oss løse følgende problem: 100011 ÷ 000101. Det første trinnet er å løse 100011 - 000101 ved å bruke 2-komplementmetoden, slik at det blir en sum:

5. Legg til 1 til kvotienten. I et dataprogram er dette punktet hvor du øker kvotienten med 1. På papiret, skriv et notat i et hjørne et sted, der det ikke vil ødelegge resten av arbeidet ditt. Vi har nå lykkes med en minsum én gang, så kvotienten så langt er 1.

6. Gjenta ved å trekke divisoren fra resten. Resultatet av vår siste beregning er resten som er igjen etter divisor én gang "gikk inn". Fortsett å legge til divisorens 2-komplement og trekke fra bæret. Legg til 1 til kvotienten hver gang, og fortsett til du får en rest lik den minste divisoren din:
Tips
- Inkrementene, dekrementeringen eller stabelinstruksjonene bør vurderes før du bruker en binær beregning på et sett med maskinsetninger.
- 2-ens komplementmetode for subtraksjon fungerer ikke hvis tallene består av et annet antall sifre. Legg til ekstra nuller til det mindre tallet for å løse dette.
- Ignorer det signerte sifferet i signerte binære tall før du gjør beregningen, bortsett fra når du prøver å finne ut om et svar er positivt eller negativt.
Artikler om emnet "Deling av binære tall"
Оцените, пожалуйста статью
Populær