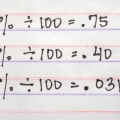Konvertering av uekte brøker til blandede tall: 9 trinn (med bilder)

Innhold

Trinn
- Metode 1 av 2: Konvertering av en uekte brøk
- Metode 2 av 2: Løse prøveproblemer
Tips

I matematikk er uekte brøker de der telleren (det øverste tallet) er større enn eller lik nevneren (det nederste tallet). For å konvertere en uekte brøk til et blandet tall (ved å bruke en brøk og et helt tall, for eksempel 2 3/4), del telleren på nevneren. Skriv hele delen av svaret ved siden av en brøk, med resten i telleren og den opprinnelige nevneren nedenfor - du har nå en blandet brøk!

Trinn

Metode 1 av 2: Konvertering av en uekte brøk

1. Del telleren med nevneren. Begynn å skrive ned den uekte brøken din. Del deretter telleren med nevneren - med andre ord, regn ut divisjonssummen som vist. Ikke glem å skrive ned resten.

La oss ta et eksempel. La oss si at vi må konvertere brøken 7/5 til et blandet tall. Vi deler først 7 med 5, for eksempel:
7/5 → 7 ÷ 5 = 1 R2

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 2

2. Skriv hele tallet til svaret. Hele tallet til det blandede tallet ditt (det store tallet til venstre for brøken din) er svaret på hele tallet til divisjonssummen. Med andre ord, bare skriv delingssvaret uten resten.

I vårt eksempel ville vi utelatt resten og bare 1 skriv det ned (siden vårt svar er 1 R2).

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 3

3. Lag en brøkdel av resten og den opprinnelige nevneren. Nå må vi finne brøkdelen av det blandede tallet. Sett resten av divisjonen inn i telleren og bruk den samme nevneren til den opprinnelige uekte brøken. Sett denne brøken ved siden av hele tallet og du har det blandede tallet!

I vårt eksempel er resten lik 2. Hvis vi setter dette som en teller over den opprinnelige nevneren (5), får vi 2/5. Vi setter dette ved siden av svaret vårt på hele tallet (1) og får det endelige blandede tallet. Følgende:

1 2/5.

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 4

4. For å gjøre dette til en uekte brøk igjen, legger vi hele tallet til telleren. Blandede tall ser bra ut på papiret og er enkle å lese, men er ikke alltid det beste valget. For eksempel, hvis vi multipliserer en brøk og et blandet tall, vil jobben vår være mye enklere hvis vi konverterer det blandede tallet tilbake til en uekte brøk. Dette gjør du ved å multiplisere hele tallet med nevneren og legge til telleren.

Hvis vi vil lage en uekte brøk fra svaret på eksempelet vårt (1 2/5), kan vi gjøre det slik:

1 × 5 = 5 → (2 + 5)/5 = 7/5

Metode 2 av 2: Løse prøveproblemer

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 5

1. Konverter 11/4 til et blandet tall. Dette problemet er enkelt - bare løs det nøyaktig som ovenfor. Se nedenfor for en trinnvis løsning.

11/4 — for å starte må vi dele telleren med nevneren.
11 ÷ 4 = 2 R 3 — nå må vi gjøre en brøkdel av resten og vår opprinnelige nevner.
11/4 = 2 3/4

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 6

2. Konverter 99/5 til et blandet tall. Vi har å gjøre med en veldig stor teller her, men ikke la det lure deg - metoden er nøyaktig den samme! Se nedenfor:

99/5 - hvor mange ganger går 5 inn i 99? Siden 5 går nøyaktig 20 ganger i 100, kan du anta at 5 går 19 ganger i 99.

99 ÷ 5 = 19 R 4 — nå lager vi bare det blandede tallet som før.

99/5 = 19 4/5

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 7

3. Konverter 6/6 til et blandet tall. Så langt har vi kun behandlet uekte brøker der telleren er større enn nevneren. Men hva skjer når begge er like? Se nedenfor for å finne ut.

6/6 — seks går en gang av seks, uten hvile, selvfølgelig.

6 6 = 1 R0. Siden en brøk med 0 i telleren alltid er lik null, trenger vi ikke å sette en brøk ved siden av hele tallet vårt.

6/6 = 1

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 8

4. Konverter 18/6 til et blandet tall. Hvis telleren er et multiplum av nevneren, ikke bekymre deg for resten - bare gjør divisjonssummen for å få svaret. Se nedenfor.

18/6 — siden vi vet at 18 bare er 6 × 3, vet vi at vi vil ha en rest av 0, så vi trenger ikke å bekymre oss for brøkdelen av vårt blandede tall.

18/6 = 3

Bilde med tittelen Konverter uekte brøker til blandede tall Trinn 9

5. Konverter -10/3 til et blandet tall. Negativer fungerer nøyaktig det samme som positive tall. Se nedenfor:

-10/3

-10 ÷ 3 = -3 R1

-10/3 = -3 1/3

Tips

Uekte brøker er ikke nødvendigvis feil. Faktisk er de noen ganger mer nyttige enn blandede tall. For eksempel, hvis du skal gange to brøker, er uekte brøker bedre fordi du bare må gange tellerne og nevnerne sammen for å få svaret ditt: f.eks. 1/6 × 7/2 = 7/12. Multipliser nå 1/6 × 3 1/2 — egentlig ikke lett.
På den annen side er blandede tall vanligvis mest nyttige når man skal beskrive noe i det virkelige liv. For eksempel krever en oppskrift 4 1/2 kopper mel, ikke 9/2 kopper mel.