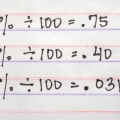Konverter brøker til desimaltall

Innhold

Trinn
Tips

Brøker og desimaler hører begge til settet med rasjonelle tall. Å konvertere brøker til desimaltall kan se forvirrende ut i begynnelsen, men når du først forstår hva brøker faktisk er, blir det mye enklere. Denne artikkelen forklarer først hva en brøk er og deretter de forskjellige måtene å konvertere en brøk til et desimaltall.

Trinn

Metode 1 av 3: Forstå brøker

1. Prøv først å forstå hva en normalbrøk er. En brøk består av tre deler: den disk, tallet over poengstreken, selve poengstreken og nevner, tallet under brøklinjen.

Nevneren angir hvor mange like deler det er i en helhet. For eksempel: en pizza kan deles i 8 stykker. Nevneren for pizzaen er da `8`.
Telleren angir tallet som deles. En skive av hele pizzaen kan representeres av en teller på `1`. Del fire med en `4` som en teller.
I dette eksemplet spiste du en del av pizzaen. Hvis du spiste ett stykke, kan det representeres med 1/8, eller en av de 8 stykkene. Har du spist tre stykker blir dette 3/8 osv.

Bilde med tittelen Konverter brøker til desimaler Trinn 2

2. Forstå desimaltallet. En desimal eller desimal, som navnet tilsier, er basert på tallet 10, akkurat som desimalsystemet. Desimalbrøker bruker ikke en skillelinje for å indikere hvilken del av helheten som menes. I stedet er helheten basert på 10, 100, 1000 osv. Brøken er representert med tallene til høyre for desimaltegnet.

Bilde med tittelen Konverter brøker til desimaler Trinn 3

3. Forstå at begge forestillingene faktisk er like. Brøker og desimaler er bare forskjellige former for en verdi mindre enn et helt tall. De ulike formene brukes avhengig av de ulike formålene folk har med å bruke dem. Vekt og størrelse uttrykkes ofte i brøker, men vitenskapelige mål (som krever større presisjon) er nesten alltid uttrykt i desimaler. Det faktum at de kan brukes om hverandre betyr at du ofte må konvertere dem for å legge til, trekke fra eller sammenligne dem.

Desimaler leses ofte på en måte som viser likheten med brøken; For eksempel uttales 0,05 høyt som "fem hundredeler", som er det samme som 5/100.

Metode 2 av 3: Konvertering av en brøk ved hjelp av lang divisjon

Bilde med tittelen Konverter brøker til desimaler Trinn 4

1. Tenk på en brøk som en divisjon. Den enkleste måten å konvertere en brøk til en desimal er å lese brøken som en divisjonssum.

2/3, for eksempel, kan også betraktes som 2 over 3; 5/8 er 5 delt på 8; og 9/10 er det samme som 9 delt på 10.
En brøk er ganske enkelt resultatet av en divisjonssum, når det som gjenstår ikke lenger er et helt tall. Telleren (toppen av brøken) blir utbyttet, nevneren (bunnen av brøken) blir divisor, og desimalen du får er resultatet.

Bilde med tittelen Konverter brøker til desimaler Trinn 5

2. Tenk på hvert siffer som en del av en kolonne. For eksempel: Tallet 23.7 har en `2` i tier-kolonnen, en `3` i en-kolonnen, og etter desimaltegnet en `7` i den tiende kolonnen (det vil si tallet så 7/10 er).

Hvis utbyttet er mindre enn deleren (eller i form av brøker, hvis telleren er mindre enn nevneren), så er tallet før desimalpunktet en 0.

For eksempel, hvis du vil konvertere brøken 3/4, blir resultatet mindre enn 1, så du får en 0 i kolonnen med enheter.

Det samme gjelder etter komma. Hvis tallet i tidelkolonnen (eller en hvilken som helst kolonne etter det) er mindre enn divisor (igjen, nevneren i brøken), legg til en 0 til resultatet og fortsett å løse.

Bilde med tittelen Konverter brøker til desimaler Trinn 6

3. Legg til en 0 på slutten av telleren. I lang divisjon må du trekke divisor fra utbytte, og det er bare mulig hvis utbytte er større enn divisor. Legg deretter til en 0 på slutten av divisoren hvis du har en 0 etter desimaltegnet, som ikke har noen effekt på utfallet.

Igjen, du kan tenke på brøken 3/4 som 3,0 ÷ 4, så du skriver det på den måten i din lange divisjon.

Bilde med tittelen Konverter brøker til desimaler Trinn 7

4. Regn ut hvor mange ganger du kan gange divisoren for å komme så nær utbyttet som mulig.

Når det gjelder 3/4, behandler du nå 3 som 30. 4 går 7 ganger på 30, og så sitter du igjen med 2. Så det første tallet i `tiendedeler`-kolonnen blir 7, og du legger til en annen `0` til resten av 2 slik at du kan gjenta prosessen igjen. 4 går inn i 20 nøyaktig 5 ganger, så resultatet i desimal er 0,75.

Metode 3 av 3: Konvertering av brøker med potenser 10 i nevneren

Bilde med tittelen Konverter brøker til desimaler Trinn 8

1. Kjenn nevnerne som har makten 10 i seg. En "potens på 10" nevner er en nevner som består av en hvilken som helst eksponent for tallet 10. Tallene 1000 eller 1000000 er potenser av 10, men i de fleste praktiske anvendelser av denne metoden vil du ha å gjøre med tallene 10, 100 eller 1000.

Bilde med tittelen Konverter brøker til desimaler Trinn 9

2. Lær å gjenkjenne de enkleste brøkene å konvertere. Enhver brøk med 5 som nevner er en klar kandidat, men brøker med nevner 25 er også veldig enkle å konvertere.

Bilde med tittelen Konverter brøker til desimaler Trinn 10

3. Multipliser med 1. Som du sikkert vet, forblir alle tall de samme når du multipliserer dem med 1. Men du kan også skrive 1 som brøk.

For eksempel er brøken 2/2 bare 1 (fordi 2 delt på 2 er lik 1). For å konvertere 1/5 til en brøk med nevneren 10, multipliser med 2/2. Svaret er da 2/10.

Du har kanskje lært at du bør forenkle brøk så mye som mulig (spesielt med partall). Dette er bare omvendt prosess, og det endrer ikke verdien av brøken.

Bilde med tittelen Konverter brøker til desimaler Trinn 11

4. Del telleren med nevneren. Du trenger ikke en vanskelig lang divisjon for dette. Alt du trenger å gjøre er å behandle telleren som et helt tall og deretter flytte desimaltegnet én plass tilbake basert på antallet nuller i nevneren.

For eksempel har du brøken 2/10. Nevneren har én 0. Så du skriver 2.0 for dette (dette endrer ikke verdien) og flytter deretter desimaltegnet ett sted til venstre. Du vil da få `0,2` som resultat.

Prøv igjen med dette nummeret: 28/1000. Nevneren har tre nuller. Vi skriver nå `28` som `28.0`. Nå flytter vi desimaltegnet tre plasser til venstre, fordi tallet har tre nuller. Så resultatet er `0,028`.

Du vil fort oppdage at du kan gjøre dette med alle slags tall som har en enkel nevner (eller en nevner som du enkelt kan lage).

Tips

Et annet ord for brøk er `brøk`, som kommer fra det latinske ordet `frangere`. Dette betyr "brudd" og det er også grunnlaget for ord som "brudd" og "fragment".