Bestill brøker etter størrelse

Innhold

Trinn
Tips

Selv om det er enkelt å bestille heltall som 1, 3 og 8 etter størrelse, er det ikke alltid åpenbart med brøker. Hvis hver nevner er like, kan du bestille dem akkurat som heltall, f.eks. 1/5, 3/5 og 8/5. I andre tilfeller kan du konvertere brøkene slik at de har samme nevner, uten å endre verdien på brøken. Dette blir lettere med øvelse, og du kan bruke noen nyttige triks, både når du sammenligner to brøker eller når du bestiller brøker der telleren er større enn nevneren, uekte brøker som 7/3.

Trinn

Metode 1 av 3: Bestilling av et hvilket som helst antall brøker

1. Finn en lik nevner for alle brøker. Bruk en av følgende metoder for å finne en nevner, eller reduser tallet på en brøk, som du kan bruke til å omskrive hver brøk i listen for enkel sammenligning. Dette er hva du kaller a fellesnevner, eller minste fellesnevner hvis dette er det minste mulig:

Multipliser hver nevner sammen. Hvis du for eksempel sammenligner 2/3, 5/6 og 1/3, multipliser disse nevnerne sammen: 3 x 6 = 18. Dette er en enkel metode, men en som ofte resulterer i et mye større antall enn de andre metodene, som er litt vanskeligere.
Eller oppgi multipler av hver nevner i en egen kolonne, til et tall som forekommer oftere skiller seg ut. For eksempel, ved 2/3, 5/6 og 1/3 har du listemultipler av 3:3, 6, 9, 12, 15, 18. Deretter en liste med multipler av 6: 6, 12, 18. Fordi 18 forekommer i begge listene, bruk det tallet (Du kan også bruke 12, men eksemplene nedenfor antar at du bruker 18).

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 2

2. Gjør om hver brøk slik at de har en lik nevner. Husk at hvis du multipliserer telleren og nevneren til en brøk med samme tall, forblir verdien av brøken den samme. Bruk denne teknikken med hver brøk, en om gangen, slik at hver brøk har samme nevner. Prøv dette for 2/3, 5/6 og 1/3, med nevneren 18:

18 ÷ 3 = 6, så 2/3 = (2x6)/(3x6)=12/18

18 ÷ 6 = 3, så 5/6 = (5x3)/(6x3)=15/18

18 ÷ 3 = 6, så 1/3 = (1x6)/(3x6)=6/18

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 3

3. Ordne brøkene etter tellerne. Nå som alle brøker har samme nevner, er de enkle å sammenligne. Bestill dem fra minste til største i henhold til telleren. Dette gir oss følgende liste: 18/6, 18/12, 15/18.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 4

4. Returner hver brøk til sin opprinnelige form. La brøkene stå i denne rekkefølgen, men konverter dem tilbake til den opprinnelige brøken. Du gjør dette ved ganske enkelt å huske hvilken brøk som tilhører hvilken eller ved å dele de øverste og nederste tallene i brøken igjen:

6/18 = (6 6)/(18 ÷ 6) = 1/3

12/18 = (12 6)/(18 ÷ 6) = 2/3

15/18 = (15 3)/(18 ÷ 3) = 5/6

Svaret er "1/3, 2/3, 5/6"

Metode 2 av 3: Ordne to brøker med kryssmultiplikasjon

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 5

1. Skriv de to brøkene side om side. Sammenlign for eksempel brøken 3/5 og brøken 2/3. Skriv disse side ved side: 3/5 til venstre og 2/3 til høyre.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 6

2. Multipliser telleren til den første brøken med nevneren til den andre. Altså: 3 x 3 = 9.

Dette kalles kryssmultiplikasjon, fordi du multipliserer tall sammen diagonalt.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 7

3. Skriv svaret ditt ved siden av den første brøken. Skriv produktet av 3 x 3 = 9, ved siden av den første brøken.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 8

4. Multipliser telleren til sekund brøk med nevneren av først. Nå for å se hvilken som er størst, sammenligner vi svaret med en annen multiplikasjon. Multipliser disse to tallene sammen. I dette eksemplet (vi sammenligner 3/5 og 2/3), multipliserer vi 2 x 5.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 9

5. Skriv svaret ved siden av den andre brøken. Skriv resultatet av 2 x 5 =10 ved siden av den andre brøken.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 10

6. Sammenlign verdiene av resultatene. Hvis den ene verdien er større enn den andre, er også brøken ved siden av resultatet størst. Så siden 9 er mindre enn 10, er 3/5 mindre enn 2/3.

Husk å alltid plassere produktet av multiplikasjonen ved siden av brøken hvis teller du brukte.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 11

7. Hvordan fungerer dette egentlig? Det du gjør er å konvertere brøkene slik at de begge har samme nevner. Så dette er hva kryssmultiplikasjon faktisk gjør! Det hopper faktisk over å skrive ned nevnerne fordi i tilfelle like nevnere trenger du bare å sammenligne tellerne. Så som følger, uten den korte ruten for kryssmultiplikasjon:

3/5=(3x3)/(5x3)=9/15

2/3=(2x5)/(3x5)=10/15

9/15 er mindre enn 10/15

Så 3/5 er mindre enn 2/3

Metode 3 av 3: Bestilling av brøker større enn én

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 12

1. Bruk denne metoden for brøker der telleren er større enn nevneren. Hvis telleren er større enn nevneren, er denne brøken større enn 1. 8/3 er et eksempel på dette. Du kan også bruke dette for brøker med samme teller og nevner, for eksempel 9/9. Dette er begge eksempler på "upassende" brøker.

Du kan fortsatt bruke de andre metodene for disse brøkene. Denne metoden vil hjelpe deg å forstå disse brøkene bedre og kan være litt raskere.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 13

2. Konverter enhver uekte brøk til en blandet brøk. Gjør det til en kombinasjon av et heltall og en brøk. Noen ganger kan du enkelt gjøre dette utenat. For eksempel, 9/9 = 1. I de vanskeligere tilfellene, bruk lang divisjon for å finne ut hvor mange ganger nevneren er delelig med telleren. Eventuell rest av den lange divisjonen forblir som en brøkdel. For eksempel:

8/3 = 2 + 2/3

9/9 = 1

19/4 = 4 + 3/4

13/6 = 2 + 1/6

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 14

3. Sorter de blandede tallene etter hele tallet. Nå som det ikke er flere uekte brøker, har du en bedre ide om størrelsen på hvert tall. Ignorer brøkene først og sorter hvert blandet tall etter heltall:

1 er den minste

2 + 2/3 og 2 + 1/6 (vi vet ikke hvilken som er større enn den andre ennå)

4 + 3/4 er størst

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 15

4. Sammenlign brøkene i hver gruppe om nødvendig. Hvis du har flere blandede tall med samme heltall, for eksempel 2 + 2/3 og 2 + 1/6, sammenligner du brøkdelen av begge tallene for å finne ut hvilken som er størst. I eksemplet sammenligner vi 2 + 2/3 og 2 + 1/6, og konverterer brøkene til samme nevner:

2/3 = (2x2)/(3x2) = 4/6

1/6 = 1/6

4/6 er større enn 1/6

2 + 4/6 er større enn 2 + 1/6

2 + 2/3 er større enn 2 + 1/6

Bilde med tittelen Bestill brøker fra minst til størst trinn 16

5. Bruk resultatet til å sortere listen over blandede tall ytterligere. Rekkefølgen på hele listen blir nå: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

Bilde med tittelen Bestill fraksjoner fra minst til størst trinn 17

6. Konverter de blandede tallene tilbake til de opprinnelige brøkene. Hold rekkefølgen den samme, men angre eventuelle endringer og skriv om brøkene som de opprinnelige uekte brøkene: 9/9, 8/3, 13/6, 19/4.

Tips

Ved sekvensering av et stort antall fraksjoner kan det være nyttig å sammenligne små grupper på 2, 3 eller 4 fraksjoner.
Selv om det kan være nyttig å finne den minste fellesnevneren, vil enhver fellesnevner fungere. Prøv å rangere 2/3, 5/6 og 1/3 med en fellesnevner på 36 og se om du får samme resultat.
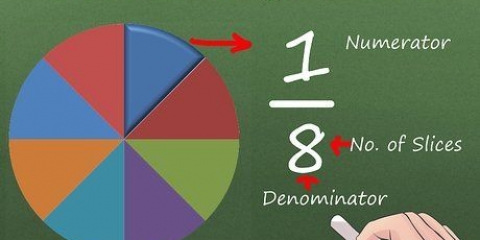
Hvis alle tellerne er like, kan du også raskt bestille brøkene. For eksempel 1/8 < 1/7 < 1/6 < 1/5. Tenk på dette som om det var en pizza: hvis du går fra 1/2 til 1/8, skjærer du pizzaen i 8 stykker i stedet for 2, og stykkene er mindre.