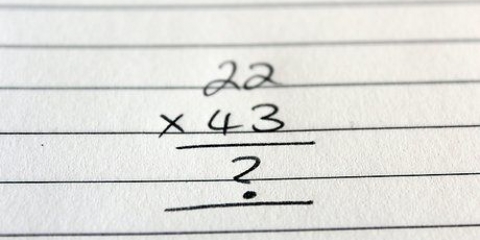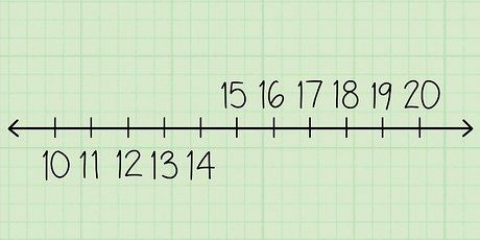Legg til og trekk fra hele tall

Innhold

Det ville du hele tall kan tenkes på som de vanlige tallene, for eksempel 3, -12, 17, 0, 7000 eller -582. Hele tall kalles også det fordi de ikke er delt inn i deler av tall, for eksempel brøker og desimaler. Les denne artikkelen for å lære alt du trenger å vite om å legge til og subtrahere heltall, eller hoppe rett til et område du trenger hjelp med.

Trinn

Metode 1 av 5: Addisjon og subtraksjon av positive heltall med tallinje

Bilde med tittelen Legg til og trekk fra heltall Trinn 1
1. Hva er en talllinje. En talllinje gjør arbeid med tall til noe virkelig og håndgripelig som du kan se for deg. Ved å bruke markører og tankene dine kan vi bruke det som en slags kalkulator for å legge til og subtrahere tall.
Bilde med tittelen Legg til og trekk fra heltall Trinn 2
2. Tegn en grunnleggende talllinje. Tegn en rett linje. Sett et merke midt på linjen. Skriv en 0 eller null ved siden av dette merket.
  • Din mattebok kan kalle dette punktet det opprinnelsespunkt, fordi dette er punktet hvor tallene kommer fra oppstår, eller start.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 3
    3. Tegn to merker, 1 på hver side av nullen. skrive -1 ved siden av markøren til venstre og 1 til høyre. Dette er heltallene nærmest null.
  • Ikke bekymre deg for mye om perfekt avstand - så lenge det ser ut som det, vil talllinjen fungere helt fint.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 4
    4. Legg til flere tall på linjen. Plasser flere markører til venstre for -1 og til høyre for 1. Følgende: -2, -3, og -4 og til høyre markeringene 2, 3, og 4, etc. så mye du kan legge på papiret.
  • Eksemplet er en nummerert linje fra -6 til 6.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 5
    5. Forstå hva positive og negative heltall er. Et positivt heltall, også kalt a naturlig tall, er et heltall større enn null. 1, 2, 3, 25, 99 og 2007 er alle positive heltall. EN negativ heltall er et heltall mindre enn null (som -2, -4 og -88).
  • Brøker som 1/2 er en del av et tall, ikke heltall. På samme måte med en desimal som 0,25; desimaler er ikke heltall.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 6
    6. Løs 1+2 ved å plassere fingeren på markøren merket 1.
  • Synes du dette er litt for enkelt? Du vil ikke være ukjent med å legge sammen, og du kan løse 1 + 2 utenat. Flott: hvis du allerede vet svaret, er det lettere å forstå hvordan talllinjen fungerer. Deretter kan du begynne å bruke en talllinje for mer kompliserte oppgaver, eller for å forberede matte og algebra.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 7
    7. Gjør summen 1+2 ved å skyve fingeren 2 merker til høyre. Tell antall markører du passerer. Har du hatt 2 merker, stopp. Tallet fingeren peker på er svaret: 3.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 8
    8. Et annet eksempel. Anta at vi vil vite hva 3 + 2 er. Start på 3, flytt til høyre og øke med 2. Vi avslutter 5. Du skriver dette som 3 + 2 = 5.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 9
    9. Trekk fra positive heltall ved å flytte til venstre på talllinjen. Som et eksempel har vi summen 6 – 4. Vi starter på 6, flytter 4 markører til venstre og avslutter på 2. Du skriver dette som 6 - 4 = 2.

    Metode 2 av 5: Legge til og trekke fra negative tall på en talllinje

    Bilde med tittelen Legg til og trekk fra heltall Trinn 10
    1. Lær hva en talllinje er. Hvis du ikke vet hvordan du lager en talllinje, gå tilbake til Legge til og subtrahere positive tall og les det igjen.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 11
    2. Forstå hva negative tall er. Positive tall er på høyre side av null og negative tall på venstre side av tallinjen. Hvis du legger til et negativt tall, flyttes fingeren til venstre på talllinjen.
  • Som eksempel tar vi summen 1 + -4. På en talllinje starter vi på 1, flytter 4 mellomrom til venstre og slutter på -3.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 12
    3. Bruk en sammenligning å forstå å legge til med et negativt tall. Merk at -3, svaret vårt, er det samme hvis vi regner ut summen 1 – 4. 1 + (-4) og 4 - 1 er det samme. Vi kan også skrive dette som en sammenligning, en matematisk måte å vise at to ting er like:

    1 + (-4) = 1 - 4 = -3
    Bilde med tittelen Legg til og trekk fra heltall Trinn 13
    4. I stedet for å legge til et negativt tall, kan vi også gjøre det til en minussum med bare positive tall. Som du kunne se fra vår enkle ligning, kan vi gå to veier - "legg til et negativt tall" eller "trekke fra et positivt tall". Du har kanskje måttet lære dette uten å bli fortalt hvorfor - her er grunnen.
  • Som et eksempel, ta -4. Hvis du legger til -4 til 1, reduserer du 1 med 4. Eller på den matematiske måten:

    1 + (-4) = 1 - 4


    Vi skriver dette på en talllinje, og setter fingeren på 1-en, så flytter du 4 mellomrom til venstre (med andre ord, legg til med -4). Siden det er en ligning, er venstre lik høyre - så det motsatte gjelder også:

    1 - 4 = 1 + (-4)

    • Bilde med tittelen Legg til og trekk fra heltall Trinn 14
    5. Forstå hvordan subtrahering av negative tall fungerer på en talllinje. På en talllinje er det å trekke fra et negativt lik å flytte til høyre. La oss starte med 5-8.
  • På en talllinje starter vi på 5, reduserer med 8 og slutter på -3. Dette er notert som

    5 - 8 = -3


    • Bilde med tittelen Legg til og trekk fra heltall Trinn 15
    6. Reduser tallet du trekker fra og se hva som skjer. Anta at summen blir 5 -7. Nå flytter vi 1 plass mindre til venstre på tallinjen. Du skriver dette som

    5 - 7 = -2
    Bilde med tittelen Legg til og trekk fra heltall Trinn 16
    7. Merk at en reduksjon kan resultere i en økning. I dette eksemplet reduserer vi antall plasser til venstre med 1. Til sammenligning blir dette:
    5 - 7 = -2 = 5 - (8 - 1)
    Bilde med tittelen Legg til og trekk fra heltall Trinn 17
    8. Gjør et minus til et pluss når du legger til negative tall. Ved å bruke trinnet "endre subtraksjon til addisjon", kan vi nå skrive dette kortere som:
    5 - (8 - 1) = 5 - 7 = 5 - 8 + 1
    .
  • Vi vet allerede at 5 - 8 = -3, så la oss utelate 5 - 8 fra ligningen vår og sette en -3 i den:
    5 - (8 - 1) = 5 - 7 = -3 + 1

  • Vi vet allerede hva 5 - (8 - 1) er - du flytter en markør mindre enn 5 - 8. Vår ligning viser at 5 - 8 = -3, og 1 trinn mindre er så -2. Nå kan ligningen vår skrives som:

    -3 - (-1) = -3 + 1

    • Bilde med tittelen Legg til og trekk fra heltall Trinn 18
    9. Skriv subtraksjonen av negative tall som et tillegg. Legg merke til hva som skjedde på slutten - vi beviste at:

    -3 + 1 = -3 - (-1)


    Vi kan uttrykke dette som en enkel, mer generell matematisk regel:

    første tall pluss et andre tall = første tall minus negativt andre tall)

    Eller, i enklere termer som i mattetimen:

    Gjør om to minuser til ett pluss
    .

    Metode 3 av 5: Legge til store positive heltall

    Bilde med tittelen Legg til og trekk fra heltall Trinn 19
    1. Skriv tillegget 2503 + 7461 med det ene tallet over det andre. Plasser tallene over hverandre, slik at 2 er over 7, 5 er over 4 osv. I denne metoden lærer vi hvordan du legger til tall som er for store til å huske eller med en talllinje.
    • Skriv et + til venstre for det nederste tallet, og en linje under det.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 20
    2. Begynn å legge til de to tallene helt til høyre. Det kan virke rart å begynne til høyre fordi vi er så vant til å lese tall fra venstre mot høyre. Vi beholder denne rekkefølgen fordi vi ellers ikke får riktig svar, som du vil se senere.
  • Under de to tallene til høyre, 3 og 1, skriv ned svaret på addisjonen av begge tallene: 4 Så.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 21
    3. Legg til hvert tall på samme måte. Arbeid fra venstre til høyre, gjør følgende tillegg: 0+6, 5+4, og 2+7. Skriv svarene under tallparene.
  • Svaret du får er, hvis du gjorde det riktig: 9964. Hvis du har gjort en feil, sjekk effekten.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 22
    4. Gjør nå summen 857+135. Her ser du en forskjell med den forrige, pga 7+5 er lik 12, et tall med 2 sifre. Men du kan ikke sette mer enn 1 siffer under et tallpar. Fortsett å lese for å lære hva du skal gjøre, og hvorfor du alltid bør begynne på høyre i stedet for til venstre.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 23
    5. Gjør summen 7 + 5 og lær hva du skal gjøre med svaret. 7+5=12, men du plasserer bare 2 under linjen og det første sifferet, 1, plassere deg ovenfor det andre tallparet, 5+3.
  • Hvis du vil vite hvordan dette fungerer, tenk på hva det betyr å dele 1 og 2. Du deler faktisk 12 i 10 og 2. Du kan skrive 10-en helt over tallene hvis du vil, deretter vil du legge merke til at 1-en stemmer overens med 5-en og 3-en, som den skal.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 24
    6. Gjør summen 1+5+3 for å få neste siffer i svaret. Du har nå 3 sifre å legge til, fordi du la til 1-en til den. Svaret er 9, så svaret ditt så langt er92.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 25
    7. Gjør oppgaven som vanlig. Fortsett å regne ut summene fra høyre til venstre til du er ferdig, legg til en kolonne til i dette tilfellet. Ditt endelige svar er 992.
  • Du kan prøve litt vanskeligere problemer, for eksempel 974+568. Husk at hver gang du får et tosifret tall, setter du kun det sene sifferet med svaret og det første sifferet over neste tallpar (neste kolonne). Hvis den siste summen har et tosifret svar, kan du plassere begge ved svaret under linjen.
  • Se på tipsene for svar på oppgaven 974+568 for å sjekke ditt eget svar.

    • Metode 4 av 5: Subtrahere store positive heltall

    Bilde med tittelen Legg til og trekk fra heltall Trinn 26
    1. Skriv summen 4713 - 502 med det første tallet over det andre. Skriv det slik at 3 er rett over 2, 1 er over 0, 7 er over 5 og 4 er over tomme plass.
    • Du kan sette en 0 under 4 hvis dette hjelper deg med å justere begge tallene. En null foran et tall endrer ikke verdien av det tallet. En null etter den gjør det, så ikke sett null der.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 27
    2. Trekk hvert nederste tall fra tallet rett over det, med start helt til høyre. Løs følgende problemer etter hverandre: 3-2, 1-0, 7-5 og 4-0. Plasser svarene rett under tallparet det tilhører.
  • Svaret bør være: 4211.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 28
    3. Gjør nå øvelsen 924 - 518 på samme måte. Disse tallene har samme lengde, så du kan enkelt justere dem. Denne øvelsen vil lære deg noe nytt om å trekke fra heltall (forhåpentligvis).
    Bilde med tittelen Legg til og trekk fra heltall Trinn 29
    4. Det første problemet, 4 - 8. Denne er vanskelig, fordi 4 er mindre enn 8, men vi kommer ikke til å bruke negative tall. Slik løser du dette:
  • Kryss ut 2-ene i det øverste tallet og skriv en 1. der. 2 er rett til venstre for 4.
  • Stryk ut 4 og gjør det til 14. Gjør dette på liten plass, slik at det er tydelig hvilket tallpar 14 tilhører, og dermed indikerer 14 – 8. Du kan også bare skrive en 1 før 4, hvis det er nok plass.
  • Det du nettopp gjorde er det "å låne" av en 1 fra kolonnen med tiere, eller også den andre kolonnen til høyre, slik at du kan legge til 10 til 4. Dette vil gi deg 14 i kolonnen med enheter.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 30
    5. Løs nå oppgave 14 - 8 og skriv svaret under høyre kolonne. Du skal nå se en 6 helt til venstre under linjen.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 31
    6. Løs neste kolonne (til venstre) med det nye tallet (2 ble erstattet av en 1). Så dette blir 1 - 1, som er lik 0.
  • Svaret ditt så langt hører hjemme 06 å være.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 32
    7. Fullfør oppgaven ved å løse den siste kolonnen. 9 - 5=4, så svaret er 406.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 33
    8. Nå går vi videre til en oppgave der vi trekker et større tall fra et mindre tall. Anta at du har 415.990 – 968.772 må løse. Du skriver det andre tallet under det første, så skjønner du at det nederste tallet er større!
  • Sørg for at tallene stemmer før du sammenligner dem. 912 er ikke større enn 5000, noe som er lett å se om tallene er riktig stilt opp, fordi 5-eren ikke står over noe. Du kan sette 1 eller flere nuller foran tallet, hvis det hjelper. Skriv for eksempel 912 som 0912 slik at den har samme lengde som 5000.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 34
    9. Skriv det minste tallet under det større tallet og sett et minustegn foran svaret. Hver gang du trekker et tall fra et mindre tall, får du et negativt tall som svar. Det er best å skrive ned minustegnet før du løser problemet, slik at du ikke glemmer det.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 35
    10. For å finne svaret, trekk det lille tallet fra det større tallet. Ikke glem minustegnet. Svaret ditt vil være negativt, som du antydet med minustegnet. Prøve ikke å trekke et større tall fra et mindre tall og deretter gjøre det negativt; på grunn av dette vil du ikke få riktig svar.
  • Det nye problemet å løse er: 968.772 - 415.990 = - ? Se på tipsene for å sjekke svaret ditt.

    • Metode 5 av 5: Addere og subtrahere negative heltall

    Bilde med tittelen Legg til og trekk fra heltall Trinn 36
    1. Lær hvordan du legger til et negativt og et positivt tall. Å legge til et negativt heltall er det samme som å trekke et positivt tall. Dette er lettere å se ved å teste dette ut med tallinjemetoden som beskrevet i et annet avsnitt, men du kan også tenke på det i ord. Et negativt tall er ikke en normal mengde; den er mindre enn null, og kan representere en mengde som tas bort. Hvis du liker dette "å fordrive" mengde til et vanlig tall, så gjør du det mindre.
    • Eksempel: 10 + -3 = 10 - 3 = 7
    • Eksempel: -12 + 18 = 18 + -12 = 18 – 12 = 6. Husk at du alltid kan bytte rekkefølge på tall i tillegg, men ikke når du trekker fra.
    Bilde med tittelen Legg til og trekk fra heltall Trinn 37
    2. Lær hva du skal gjøre når det blir en minussum med det minste tallet. Noen ganger kan det skje at å konvertere en sum til en minussum gir resultater som 4 – 7. Hvis dette skjer, snu tallene og gjør svaret negativt.
  • Anta at du har 4 + -7.
  • Gjør dette til en minussum: 4 - 7
  • Snu rekkefølgen og gjør summen negativ: -(7 – 4) = -(3) = -3.
  • Hvis du ikke er vant til å bruke parentes i summene dine, tenk på det slik: 4 - 7 blir 7 - 4 og legg til et minustegn. Så 7 - 4 = 3 og så gjør du det -3 for å få riktig svar på summen 4 - 7.
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 38
    3. Lær hvordan du legger til to negative heltall. To negative tall lagt sammen gjør alltid svaret negativt og større. Det legges ikke til noe positivt, så du ender alltid opp med noe enda lenger fra null. Det er enkelt å finne svaret:
  • -3 + -6 = -9
  • -15 + -5 = -20
  • Ser du mønsteret? Alt du trenger å gjøre er å legge tallene sammen som om de var positive og deretter legge til et negativt tegn til dem. -4 + -3 = -(4 + 3) = -7
    • Bilde med tittelen Legg til og trekk fra heltall Trinn 39
    4. Lær hvordan du trekker fra et negativt heltall. Som med plusssummene kan du skrive om disse slik at du kun har med positive tall å gjøre. Hvis du trekker fra et negativt tall, da "tar du bort noe" av "noe som blir tatt bort", som er det samme som å legge til et positivt tall.
  • Tenk på et negativt tall som stjålne penger. hvis du noe "rykker av", eller tar bort fra de stjålne pengene for å returnere dem, det er det samme som å gi penger til den personen, eller ikke?
  • Eksempel: 10 – -5 = 10 + 5 = 10
  • Eksempel: -1 – -2 = -1 + 2. Du har allerede lært hvordan du løser dette, i et tidligere trinn, husk? lese på nytt "Lær hvordan du legger til et negativt og et positivt tall" hvis du ikke vet.
  • Her er den fullstendige løsningen av det siste eksemplet: -1 – -2 = -1 + 2 = 2 + -1 = 2 – 1 = 1.

    • Tips

    • Du er sannsynligvis vant til å skrive lange tall som 2.521.301. I mange land er det vanlig å bruke komma i stedet for punktum, eller omvendt (for desimaler). Ikke la det forvirre deg når du søker på internett etter informasjon om dette emnet. Hold deg til det du lærer om dette på skolen.
    • Lag forskjellige talllinjer for forskjellige tall. Det er ikke en regel at talllinjer alltid går over heltall. Dette kan også dreie seg om tiere, eller brøker. Bortsett fra at hvert mellomrom nå representerer noe forskjellig, kan du fortsatt bruke tallinjen for addisjon og subtraksjon på samme måte. Gi det et forsøk.
    • Hvis du prøvde det ekstra problemet i delen med store tall, her er svarene: 974 + 568 = 1542. Svaret på summen 415.990 – 968.772 er -552.782.

    no.FaqCartx.info / Utdanning og kommunikasjon
    Оцените, пожалуйста статью
    Ny
    Velg din livspartner
    Velg din livspartner
    Beregn arealet av en ellipse
    Beregn arealet av en ellipse
    Last ned raskere med internet download manager (idm)
    Last ned raskere med internet download manager (idm)
    Dressing for en stor byste
    Dressing for en stor byste
    Bruker blodmåltid
    Bruker blodmåltid
    Lader en kindle
    Lader en kindle