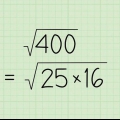Faktorering av et tall: 11 trinn (med bilder)

Innhold

Trinn
- Metode 1 av 2: Faktorisering av heltall
- Metode 2 av 2: Big Number Factoring-strategi
Tips
Advarsler
Nødvendigheter

Faktorene til et gitt produktnummer er de tallene som, når de multipliseres sammen, gir det produktet. En annen måte å tenke på dette er at hvert tall er et produkt av flere faktorer. Å lære å faktorisere er en viktig matematisk ferdighet, brukt ikke bare i aritmetikk, men også i algebra, analyse og andre matematiske felt. Les videre for å lære mer om faktorisering!

Trinn

Metode 1 av 2: Faktorisering av heltall

1. Skriv ned nummeret. Du kan faktorisere hvilket som helst tall, men for enkelhets skyld starter vi med et heltall. Hele tall er positive eller negative tall uten brøker eller desimaler.

ta nummeret 12. Skriv dette på et stykke papir.

Bilde med tittelen Factor a Number Step 2

2. Finn ytterligere to tall som multiplisert sammen danner det første tallet som et produkt. Ethvert heltall kan skrives som produktet av to andre heltall. Selv primtall kan skrives som produktet av 1 og selve primtallet. Å tenke i forhold til faktorer krever en annen måte å resonnere på. Du spør faktisk deg selv, "hvilken multiplikasjon er lik dette tallet?"

I vårt eksempel har 12 flere faktorer - 12 × 1, 6 × 2 og 3 × 4 - alle er lik 12. Så det kan vi si 1, 2, 3, 4, 6 og 12 er alle faktorer på 12. For vårt formål er det tilstrekkelig å fortsette med faktorene 6 og 2.

Partall er spesielt lette å faktorisere, fordi disse tallene alltid har en faktor på 2. 4 = 2 × 2, 26 = 13 × 2, osv.

Bilde med tittelen Factor a Number Trinn 3

3. Bestem om de valgte faktorene kan løses opp igjen selv. Mange tall – spesielt de større – kan faktoriseres flere ganger. Avhengig av situasjonen kan du ha nytte av dette eller ikke.

For eksempel faktoriserte vi 12 til 2 × 6. Merk at 6 igjen kan faktoriseres inn i faktorene 3 × 2 = 6. Så vi kan si at 12 = 2×(3×2).

Bilde med tittelen Faktor et tall Trinn 4

4. Slutt å faktorisere når du møter en primfaktor. Primtall er tall som er delbare med 1 og seg selv. For eksempel 1, 2, 3, 5, 7, 11, 13 og 17 er alle primtall. Hvis du har faktorisert et tall til det punktet hvor det bare er primtall igjen, er det ingen vits i å fortsette, fordi de eneste faktorene som er igjen er 1 og selve primtallet.

I vårt eksempel løste vi opp 12 og forenklet det til 2 × (2 × 3). 2, 2 og 3 er alle primtall. Hvis vi skulle gå enda lenger, ville vi måtte faktorisere (2 × 1) × ((2 × 1)(3 × 1)), noe som ikke lenger er til noen nytte for deg..

Bilde med tittelen Factor a Number Step 5

5. Løs negative tall på samme måte. Negative tall kan faktoriseres på nesten samme måte som positive tall. Den store forskjellen er at faktorene multiplisert sammen må få et negativt tall som produktet, så et oddetall av faktorene må være negative.

La oss faktor 60 som et eksempel. Se lenger nedenfor:

-60 = -10 × 6

-60 = (-5 × 2) × 6

-60 = (-5 × 2) × (3 × 2)

-60 = -5×2×3×2. Merk at å ha et oddetall negative tall ved siden av 1-en, returnerer det samme produktet. For eksempel, -5 × 2 × -3 × -2 er også lik 60.

Metode 2 av 2: Big Number Factoring-strategi

Bilde med tittelen Factor a Number Step 6

1. Skriv nummeret ditt øverst i en tabell med 2 kolonner. Selv om det vanligvis er veldig enkelt å faktorisere mindre tall, kan noen ganger større tall være ganske skremmende. De fleste av oss ville ha vanskelig for å faktorisere et 4- eller 5-sifret tall uten annet enn hjernen din. Heldigvis blir dette mye enklere ved hjelp av et bord.

Velg et 4-sifret tall for å faktorisere - 6552.

Bilde med tittelen Factor a Number Step 7

2. Del tallet ditt med den minste mulige primfaktoren, bortsett fra 1. Skriv primtallet i venstre kolonne og svaret i neste kolonne. Som beskrevet ovenfor er partall de enkleste å faktorisere fordi det minste primtallet (unntatt 1) alltid er lik 2. Oddetall har derimot forskjellige minste primfaktorer.

I vårt eksempel vet vi at 2 er den minste primfaktoren, fordi 6552 er et partall. 6552 2 = 3276. I venstre kolonne skriver vi 2 og til høyre 3276.

Bilde med tittelen Factor a Number Step 8

3. Fortsett faktoriseringen på denne måten. Faktorer nå tallet i høyre kolonne og finn den minste primfaktoren av dette tallet. Skriv det under forrige primfaktor i venstre kolonne og det nye tallet i høyre kolonne. Fortsett slik til du ikke klarer å løse lenger (tallet i høyre kolonne blir mindre og mindre).

Så for å fortsette vårt eksempel: 3276 ÷ 2 = 1638, så i venstre kolonne skriver vi en annen 2 og i høyre kolonne 1638. 1638 ÷ 2 = 819, så vi skriver 2 og 819 i venstre og høyre kolonne.

Bilde med tittelen Factor a Number Step 9

4. Behandle oddetall ved alltid å starte med de minste primfaktorene. For oddetall kan det minste primtall avvike, i motsetning til partall hvor 2 alltid er det minste primtall (unntatt 1). Start med primfaktorer som 3, 5, 7, 11 og så videre til du finner en som er en faktor av tallet ditt. Dette er den minste primfaktoren.

I vårt eksempel ser vi at 819 er oddetall og derfor ikke kan ha en primfaktor på 2. Så la oss prøve en annen prime. 819 ÷ 3 = 273 uten rest, så 3 er den minste primfaktoren på 819 og vi fortsetter med 273.

Når du ser etter faktorer, prøv alle primtall opp til kvadratroten av den største faktoren du fant. Hvis ingen av tallene du prøver er en divisor av den største faktoren, så er den største divisoren i seg selv sannsynligvis primtall, så du er ferdig med å faktorisere.

Bilde med tittelen Factor a Number Step 10

5. Fortsett til du kommer til 1. Fortsett å finne den minste primtall av tallene i høyre kolonne til du står igjen med et primtall i den høyre kolonnen. Dette deler du så på seg selv, slik at tallet vises i venstre kolonne og en "1" i høyre kolonne.

La oss nå fullføre dekomponeringen. se nedenfor for detaljer:

Del igjen med 3: 273 ÷ 3 = 91, ingen rest, så vi skriver 3 og 91.

La oss prøve en 3-er igjen: dette fungerer ikke for 91, og det fungerer heller ikke med 5 (neste primtall), men 91 ÷ 7 = 13 fungerer, uten rest, så vi skriver 7 og 1. 3.

La oss prøve 7 igjen: 13 har verken 7 eller 11 som faktor, men seg selv: 13 ÷ 13 = 1.Så for å lukke dette bordet, merker vi 1. 3 og 1. Vi kan endelig stoppe factoring.

Bilde med tittelen Factor a Number Step 11

6. Tallene i venstre kolonne er dine faktorer. Dette betyr at produktet av en multiplikasjon av disse tallene må være lik tallet øverst i tabellen. Hvis den samme faktoren forekommer mer enn én gang, skriv den som en kraft av den faktoren for å spare plass. For eksempel, hvis i listen over faktorer 2 forekommer fire ganger, skriv det som 2 i stedet for 2 × 2 × 2 × 2.

Så i vårt eksempel skriver vi som følger: 6552 = 2×3×7×13. Dette er den fullstendige primfaktoriseringen av 6552. Så produktet av multiplikasjonen av disse tallene er 6552.

Tips

1-en er ikke et primtall, men et spesialtilfelle.
De første primtallene er 2, 3, 5, 7, 11, 13, 17, 19 og 23.
Forstå at et tall er en faktor av et annet, større tall, hvis dette tallet er helt delelig med faktoren; så uten en rest igjen. For eksempel er tallet 6 en faktor på 24, fordi 24 ÷ 6 = 4, uten rest.6 er derfor ikke en faktor på 25.
Hvis tallene i telleren summeres til et multiplum av tre, er tre en faktor av det tallet. ( 819 = 8+1+9 = 18 = 1+8 =9.Tre er en faktor på ni, så det er også en faktor på 819)
Noen tall kan faktoriseres raskere, men denne måten fungerer alltid og en ekstra fordel er at primfaktorene er oppført i stigende rekkefølge når du er ferdig.
Husk at vi bare snakker om heltall som 1, 2, 3, 4, 5...og ikke om brøker eller desimaltall, som ligger utenfor denne artikkelens omfang.

Advarsler

Ikke gjør det for vanskelig for deg selv. Hvis du har utelukket en faktor, ikke fortsett å sjekke i det uendelige. Når du har oppdaget at 2 ikke kan være en faktor på 819, fortsett med å vite at du ikke trenger å vurdere 2 som en faktor igjen.