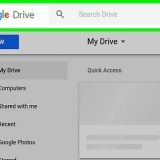
Areal = 1/2 x (3 cm x 5 cm) 
Areal = 1/2 x (3 cm x 5 cm) Overflate = 1/2 x 15 cm Areal = 7.5 cm 

Areal = √{6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Areal = √{6 (3)(2)(1)} 









Areal = 1/2(b)(c) x sin A Areal = 1/2(150)(231) x sin A 
Areal = 1/2(150)(231) x sin A Areal = 1/2(34 650) x sin A Areal = 17.325 x sin A Areal = 17 325 x .8386705 Areal = 14.530 cm
Regn ut arealet til en trekant
Innhold
Selv om den vanligste metoden for å beregne arealet til en trekant er å multiplisere dens halve base med høyden, er det en rekke andre måter å beregne arealet av en trekant på, avhengig av tilgjengelige data. Dette inkluderer lengden på alle tre sidene, lengden på den ene siden av en likesidet trekant, og lengden på to sider sammen med den inkluderte vinkelen. Les her hvordan du kan beregne arealet til en trekant ved hjelp av disse dataene.
Trinn
Metode 1 av 4: Med basen og høyden

1. Bestem bunnen og høyden til trekanten din. Basen til trekanten er lengden på den ene siden, som vanligvis er undersiden av trekanten. Høyde er lengden fra basen til det øverste hjørnet av trekanten, som er vinkelrett på basen. I en rettvinklet trekant er basen og høyden de to sidene som møtes i en 90-graders vinkel. Men i en annen trekant, som vist nedenfor, vil høydelinjen skjære rett gjennom formen.
- Når du har bestemt bunnen og høyden til trekanten, er du klar til å begynne å bruke formelen.

2. Skriv ned formelen for å finne arealet av en trekant. Formelen for denne typen problemer er Areal = 1/2 (grunnlag x høyde), eller 1/2 (bh). Når du har notert alt, kan du begynne å fylle ut lengden på høyden og basen.

3. Angi grunn- og høydeverdier. Finn basen og høyden til trekanten og bruk disse verdiene i ligningen. I dette eksemplet er høyden på trekanten 3 cm og bunnen av trekanten er 5 cm. Slik vil formelen se ut etter å ha lagt inn disse verdiene:

4. Løs ligningen. Du kan gange høyden ganger basen først fordi disse verdiene er i parentes. Deretter multipliserer du resultatet med 1/2. Husk at du skal gi svaret i kvadratmeter fordi du arbeider i todimensjonalt rom. Slik løser du dette for det endelige svaret:
Metode 2 av 4: Bruk av lengden på hver side (Heron`s Formula)

1. Regn ut den halve omkretsen (semiperimeter) til trekanten. For å finne den halve omkretsen av trekanten trenger du bare å legge alle sidene sammen og dele resultatet på to. Formelen for å finne den halve omkretsen av en trekant er som følger: semiperimeter = (lengde på side a + lengde på side b + lengde på side c) / 2, eller s = (a + b + c) / 2. Siden alle tre lengdene av den rette trekanten er gitt, 3 cm, 4 cm og 5 cm, kan du plugge disse direkte inn i formlene og løse oppgaven for den halve omkretsen:
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6

2. Skriv inn de riktige verdiene i formelen for å finne arealet til en trekant. Denne formelen for å finne arealet av en trekant kalles også Herons formel og går slik: Areal = √{s (s - a)(s - b)(s - c)}. Vi gjentar forrige trinn hvor s den halve omkretsen er og en, b, og c de tre sidene av trekanten. Benytt deg av følgende operasjonssekvens: start med å løse alt innenfor parentesen, deretter alt under det radikale tegnet, og til slutt selve kvadratroten. Slik vil denne formelen se ut når du har angitt alle kjente verdier:

3. Trekk fra verdiene innenfor parentesen. Altså: 6 - 3, 6 - 4 og 6 - 5. Her er resultatet på papir:

4. Multipliser resultatene av disse operasjonene. Multipliser 3 x 2 x 1 for å få 6 som svar. Du må gange disse tallene sammen før du multipliserer dem med 6 fordi de står i parentes.

5. Multipliser det forrige resultatet med halvparten av omkretsen. Multipliser deretter resultatet, 6, med den halve omkretsen, som også er 6. 6 x 6 = 36.

6. Regn ut kvadratroten. 36 er et perfekt kvadrat og √36 = 6. Ikke glem enheten du startet med -- centimeter. Uttrykk det endelige svaret i kvadratcentimeter. Arealet av trekanten med sidene 3, 4 og 5 er 6 cm.
Metode 3 av 4: Bruk av den ene siden av en rektangulær trekant

1. Finn siden til den likesidede trekanten. En likesidet trekant har like lange sider og like vinkler. Du vet at du har å gjøre med en likesidet trekant, enten fordi dette er gitt, eller fordi du vet at alle vinkler og alle sider har samme verdi. Verdien av en av sidene i denne trekanten er 6 cm. Legg merke til dette.
- Hvis du vet at du har å gjøre med en likesidet trekant, men bare omkretsen er kjent, deler du denne verdien på 3. For eksempel er lengden på den ene siden av en likesidet trekant med omkrets 9 ganske enkelt 9/3, eller 3.

2. Skriv ned formelen for å finne arealet av en likesidet trekant. Formelen for denne typen problemer er areal = (s^2)(√3)/4. Noter det s "silke" betyr.

3. Bruk verdien av en side på ligningen. Beregn først kvadratet på siden med verdi 6, for å få 36. Finn så verdien av √3, hvis svaret skal gis i desimaler. Skriv nå inn √3 i kalkulatoren for å få 1.732 å få. Del dette tallet med 4. Merk at du også kan dele 36 med 4 og deretter multiplisere med √3 -- rekkefølgen på operasjonene har ingen innvirkning på svaret.

4. Løse. Nå handler det i hovedsak om å bare telle. 36 x √3/4 = 36 x .433 = 15.59 cm Arealet av en likesidet trekant med en side på 6 cm er 15.59 cm.
Metode 4 av 4: Bruk av lengden på to sider og den inkluderte vinkelen

1. Finn verdien av lengdene på to sider og den inkluderte vinkelen. Den inkluderte vinkelen er vinkelen mellom de to kjente sidene av trekanten. Du må kjenne disse verdiene for å finne arealet til en trekant ved å bruke denne metoden. La oss anta en trekant med følgende dimensjoner:
- vinkel A = 123º
- side b = 150 cm
- side c = 231 cm

2. Skriv ned formelen for å finne arealet av trekanten. Formelen for å finne arealet til en trekant med to kjente sider og en kjent inkludert vinkel er som følger: Areal = 1/2(b)(c) x sin A. I denne ligningen representere "b" og "c" lengdene på sidene og "en" hjørnet. Du bør alltid ta sinus til vinkelen i denne ligningen.

3. Fyll inn verdiene i ligningen. Slik ser ligningen ut etter at du har skrevet inn disse verdiene:

4. Løse. For å løse denne ligningen, multipliser først sidene og del resultatet på to. Multipliser deretter dette resultatet med sinusen til vinkelen. Verdien av sinusen finner du med kalkulatoren. Ikke glem å gi svaret i kubikkenheter. Slik gjør du det:
Tips
- Hvis du ikke forstår hvorfor den grunnleggende høydeformelen fungerer på denne måten, her er en kort forklaring. Hvis du lager en andre, identisk trekant og legger den ved siden av hverandre, vil den enten danne et rektangel (to rette trekanter) eller et parallellogram (to ikke-rette trekanter). Alt du trenger å gjøre for å finne arealet til et rektangel eller parallellogram er å multiplisere grunnflaten med høyden. Siden en trekant er lik et halvt rektangel eller parallellogram, følger det at arealet av en trekant er lik en halv base ganger høyden.
Artikler om emnet "Regn ut arealet til en trekant"
Оцените, пожалуйста статью
Populær