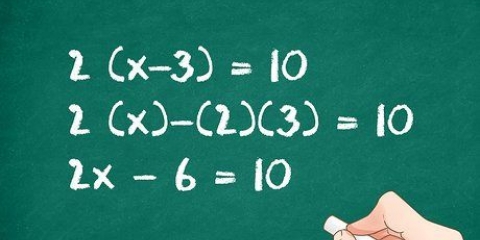x=-b/2a x=-(9)/(2)(1) x=-9/2 
y = x + 9x + 18 y = (-9/2) + 9(-9/2) +18 y = 81/4 -81/2 + 18 y = 81/4 -162/4 + 72/4 y = (81 - 162 + 72)/4 y = -9/4 



x + 4x + 1 = 0 x + 4x + 1 -1 = 0 - 1 x + 4x = - 1 
(4/2) = 2 = 4. Legg nå til 4 på begge sider av ligningen for å få følgende: x + 4x + 4 = -1 + 4 x + 4x + 4 = 3 

Finne ekstremverdien til en ligning
Innhold
Den ekstreme verdien av en parabel er maksimum eller minimum av ligningen. Hvis du vil finne ekstremverdien til en kvadratisk ligning, bruk en formel eller løs ligningen. Her vil du lære hvordan du gjør det.
Trinn
Metode 1 av 2: Formelen x = -b/2a

1. Bestem verdiene til a, b og c. I en andregrads- eller andregradsligning,X = en,X = b, og konstanten (leddet uten variabel) = c. Anta at vi har å gjøre med følgende ligning: y = x + 9x + 18. I dette eksemplet, en = 1, b = 9 og c = 18.

2. Bruk en formel for å finne verdien av x. Toppunktet til parabelen er også symmetriaksen til ligningen. Formelen for å finne ekstremverdien x av en kvadratisk ligning er x = -b/2a. Fyll inn de relevante verdiene i denne ligningen for å få X å finne. Bytt ut verdiene med a og b. Dette er hvordan:

3. Plugg verdien av x inn i den opprinnelige ligningen for å få verdien av y. Nå som du vet x er det mulig å bruke denne verdien på den opprinnelige ligningen for å få y. Formelen for å bestemme ekstremverdien til en kvadratisk ligning er (x, y) = [(-b/2a), f(-b/2a)]. Dette betyr bare at for å få y, kan du finne x ved å bruke denne formelen og deretter koble den inn i den opprinnelige ligningen. Slik går det:

4. Skriv verdiene for x og y som et ordnet par. Nå som du vet at x = -9/2 og y = -9/4, skriv bare disse verdiene som et ordnet par: (-9/2, -9/4). Ekstremverdien til denne kvadratiske ligningen er (-9/2, -9/4). Hvis du ønsket å tegne denne parabelen i en graf, så er dette punktet minimum av parabelen, fordi x er positiv.
Metode 2 av 2: Utarbeide ligningen

1. Skriv ligningen. Å regne ut ligningen er en annen måte å finne den ekstreme verdien av en kvadratisk ligning. Med denne metoden er det mulig å finne x- og y-koordinatene umiddelbart. La oss si at vi jobber med følgende kvadratiske ligning: x + 4x + 1 = 0.

2. Del hvert ledd med koeffisienten til x . I dette tilfellet er koeffisienten ofx lik 1, så du kan hoppe over dette trinnet. Å dele hvert ledd med 1 spiller ingen rolle!

3. Flytt konstanten til høyre side av ligningen. Konstanten er leddet uten koeffisient. I dette tilfellet altså "1". Flytt 1-en til den andre siden av ligningen ved å trekke 1 fra begge sider. Slik gjør du det:

4. Fullfør kvadratet til venstre for ligningen.Arbeid (b/2) og legg resultatet til begge sider av ligningen. fylle "4" inn som verdi av b, fordi "4x" b-leddet er av ligningen.

5. Faktor venstre side av ligningen. Nå vil du se at x + 4x + 4 er et perfekt kvadrat. Dette kan skrives om som (x + 2) = 3

6. Bruk dette til å finne x- og y-koordinatene. Du kan finne x-koordinaten ved å gjøre (x + 2) lik null. Så hvis (x + 2) = 0, hva skal x være? Variabelen x må da være lik -2 for å kompensere for +2, så x-koordinaten er -2. Y-koordinaten er ganske enkelt konstantleddet på den andre siden av ligningen. Så y = 3. Du kan også ta en snarvei og ta fortegnet til tallet i parentes for å finne x-koordinaten. Så ekstremverdien av ligningen x + 4x + 1 = (-2, 3)
Tips
- Forstå hva a, b og c representerer.
- Vis arbeidet ditt og sjekk det! Som et resultat vet læreren din at du forstår, og du har selv sjansen til å se og rette feil i svarene dine.
- Følg denne rekkefølgen for behandling for å garantere et godt resultat av oppdraget.
Advarsler
- Sørg for at du forstår hva a, b og c representerer - ellers blir ikke svaret riktig.
- Ikke bekymre deg – øvelse gjør mester.
Nødvendigheter
- Grafpapir eller datamaskin
- Kalkulator
Artikler om emnet "Finne ekstremverdien til en ligning"
Оцените, пожалуйста статью
Populær