Memorering av enhetssirkelen: 14 trinn (med bilder)

Innhold

Trinn
- Del 1 av 2: Husk radianene
- Del 2 av 2: Husk x- og y-koordinatene (cosinus, sinus)
Tips

Å lære enhetssirkelen vil hjelpe deg ikke bare med trigonometri og geometri, men også med differensial- og integralregning. Det kan virke som mye memorering, men når du først forstår hvordan det fungerer, kan du begynne med noen tall fra enhetssirkelen og raskt finne ut resten.

Trinn

Del 1 av 2: Husk radianene

1. Tegn to vinkelrette linjer. Plasser et kompass på et stort ark. Tegn en vertikal og en horisontal linje. Disse skal krysse hverandre nær midten av siden. Dette er x-aksen og y-aksen til grafen.

Bilde med tittelen Memorize the Unit Circle Trinn 2

2. Tegn en sirkel. Bruk et kompass til å tegne en stor sirkel sentrert i skjæringspunktet mellom de to linjene.

Bilde med tittelen Memorize the Unit Circle Trinn 3

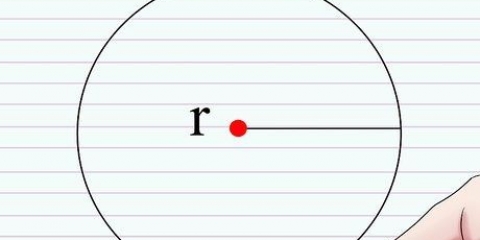
3. Forstå radianer. En radian er et vinkelmål. Det er hovedsakelig definert på en slik måte at en person som går rundt en sirkel med en Stråle på 1 enhet beveger seg gjennom en vinkel på en radian etter å ha gått 1 enhet rundt omkretsen. I neste trinn vil vi indikere de fire koordinatpunktene med radianverdien. Hvis du husker formelen for forholdet mellom en sirkels omkrets og radius, kan du regne ut det raskt, men selv om du ikke husker det.

Radianmålingene til enhetssirkelen forutsetter alltid at du starter fra punktet (0, 1). For å gjøre det klart hvilket punkt vi sikter til, beskriver vi sirkelen som en kompassrose:

Bilde med tittelen Memorize the Unit Circle Trinn 4

4. Husk at sirkelens omkrets er 2π. Omkretsen til en sirkel er lik 2πr, hvorved r står for radius (radius). Siden enhetssirkelen har en radius på 1, kan vi forenkle omkretsen til 2π. Radianverdien til ethvert punkt på omkretsen kan du finne ved å dele 2π på den delen av sirkelen du hadde. Dette er mye enklere enn å huske hver enkelt verdi på sirkelen.

Bilde med tittelen Memorize the Unit Circle Trinn 5

5. Angi de fire punktene på x- og y-aksene. Alt du trenger å gjøre er å dele 2π i kvartaler:

`Øst` er utgangspunktet, så du har 0 hadde radianer.

`Nord` = en fjerdedel av sirkelens omkrets = /₄ = /₂ radianer.

`Vest` = halvveis gjennom sirkelen = /₂ = π radianer.

`Sør` = tre fjerdedeler av sirkelen = 2π * ¾ = /₂ radianer.

Går du langs hele omkretsen går du tilbake til utgangspunktet. Du kan angi dette som 2π eller 0.

Bilde med tittelen Memorize the Unit Circle Trinn 6

6. Del sirkelen i åtte deler. Tegn nå en diagonal linje gjennom hver kvadrant, perfekt gjennom midten. Igjen, bruk divisjon for å finne verdien i radianer:

/₄

(π/2, π, 3π/2 og 2π er allerede indikert.)

Bilde med tittelen Memorize the Unit Circle Trinn 7

7. Del sirkelen i seks segmenter. Tegn nå flere linjer som deler sirkelen i seks segmenter. (Du kan bruke en gradskive for dette, med start på den positive x-aksen, hvor hvert segment måler 60 grader). Du kan bruke samme tilnærming som ovenfor for å sikre at en sjettedel av en sirkel er lik /₆ = /₃ radianer. Bruk denne etiketten for følgende punkter på omkretsen (ett i hver kvadrant):

/₃

(π og 2π er allerede indikert)

Bilde med tittelen Memorize the Unit Circle Trinn 8

8. Tegn tolvdeler i den. De siste punktene som er merket på de fleste enhetssirkler indikerer trinn på en tolvtedel av omkretsen. Bare fire av disse er ennå ikke erklært:

/₆

Del 2 av 2: Husk x- og y-koordinatene (cosinus, sinus)

Bilde med tittelen Memorize the Unit Circle Trinn 9

1. Forstå cosinus og sinus. Enhetssirkelen er spesielt nyttig for trigonometriske beregninger med rette vinkler. Enhver x-koordinat til et punkt på sirkelen er lik cos(θ) og enhver y-koordinat er lik sin(θ), der θ er verdien av vinkelen.

Hvis du synes det er vanskelig å huske, tenk på (cos, sin) "fordi sinus kommer sist".
Du kan utlede dette ved å bruke rette trekanter og definisjonen av disse funksjonene - husk `soscastoa`?

Bilde med tittelen Memorize the Unit Circle Trinn 10

2. Skriv ned koordinatene ved fire punkter i sirkelen. En `enhetssirkel` er ganske enkelt en sirkel med en radius på nøyaktig én enhet. Bruk disse til å finne x- og y-koordinatene til de fire punktene på sirkelen der den skjærer en akse. (Vi kaller disse `Øst`, `Nord` osv. for enkel lesing, men dette er ikke offisielle navn).

Koordinatene til `Øst` er (1, 0).

Koordinatene til `Nord` er (0, 1).

Koordinatene til `Vest` er (-1, 0).

Koordinatene til `Sør` er (0, -1).

Dette fungerer akkurat som en vanlig graf. Du skal kunne finne disse koordinatene selv, uten å måtte huske dem.

Bilde med tittelen Memorize the Unit Circle Step 11

3. Husk koordinatene til den første kvadranten. Den første kvadranten er den øvre høyre fjerdedelen av sirkelen, hvor både x-verdier som y-verdiene er positive. Dette er de eneste koordinatene du trenger å huske:

På /₆, er koordinatene ( $\frac{\sqrt{3}}{2}, \frac{1}{2}$ ${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ).

På /₄, er koordinatene ( $\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}$ ${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ).

På /₃, er koordinatene ( $\frac{1}{2}, \frac{\sqrt{3}}{2}$ ${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Merk at det kun er tre tellere. Beveger du deg i en positiv retning (venstre til høyre for x-verdier, fra bunn til topp for y-verdier), så er sekvensen som følger: 1 → √2 → √3.

Bilde med tittelen Memorize the Unit Circle Step 12

4. Tegn rette linjer for å fylle ut de andre koordinatene. Hvis du kan tegne en perfekt vertikal eller en perfekt horisontal linje mellom to punkter, så har de samme absolutte verdi som x- og y-koordinater. Du kan med andre ord tegne en linje fra et punkt i de første kvadrantene, skrive de samme koordinatene på punktet der du lander, og la plass til høyre for tegnet (+ eller -).

Du kan for eksempel tegne en horisontal linje mellom /₃ og /₃. Siden koordinatene ved det første punktet (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ), koordinatene til det andre punktet (?

\frac{1}{2}, ? \frac{\sqrt{3}}{2}

${frac{1}{2}},?{frac{{sqrt{3}}}{2}}$ ), hvorved `?` representerer et pluss- eller minustegn (+ eller -).

Her er en raskere måte: Sjekk nevneren til radianene. Alle punkter som slutter på /3 har de samme absolutte koordinatene, akkurat som alle punkter som slutter på /4 og alle punkter som slutter på /6.

Bilde med tittelen Memorize the Unit Circle Step 13

5. Bruk symmetri for å finne ut om tegnet er positivt eller negativt. Det er flere måter å huske hvor du skal plassere minustegn på enhetssirkelen:

Tenk grunnleggende regler for diagrammer. Over X-aksen er punktene positive, under den negative. Til venstre for y er negativ, rett er positivt.

Start fra kvadrant 1 og tegn linjer til andre punkter. Hvis linjen de y-aksen krysser y-verdien vil bytte fortegn. Hvis linjen de X-akse krysser, så endrer x-verdien fortegn.

Lær `All Students Test Calculus` (ASTC), mot klokken. Kvadrant 1 har enbare positive verdier, kvadrant 2 har bare positive verdier sinus-verdier, har kvadrant 3 kun positive tangens verdier, og kvadrant 4 har bare positive Cosine verdier.

Uavhengig av metoden du velger, er tegnene (+, +) for kvadrant 1, (-, +) for kvadrant 2, (-, -) for kvadrant 3 og (+,-) for kvadrant 4.

Bilde med tittelen Memorize the Unit Circle Step 14

6. Sjekk arbeidet ditt. Her er den fullstendige listen over koordinatverdier for hvert merkede punkt på sirkelen (ikke teller de fire punktene på aksene), med klokken. Husk at du skal kunne finne alle disse verdiene bare ved å huske punktene i kvadrant 1:

Kvadrant 1: (

\frac{\sqrt{3}}{2}, \frac{1}{2}

${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ); (

\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Kvadrant 2: (

- \frac{1}{2}, \frac{\sqrt{3}}{2}

$-{frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ); (

- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

- \frac{\sqrt{3}}{2}, \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},{frac{1}{2}}$ )

Kvadrant 3: (

- \frac{\sqrt{3}}{2}, - \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ ); (

- \frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

- \frac{1}{2}, - \frac{\sqrt{3}}{2}

$-{frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ )

Kvadrant 4: (

\frac{1}{2}, - \frac{\sqrt{3}}{2}

${frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ ); (

\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

\frac{\sqrt{3}}{2}, - \frac{1}{2}

${frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ )

Tips

Hvis du har en test eller repetisjon på enhetssirkelen, tegn først sirkelen på utklippspapir slik at du kan bruke den som referanse for hver oppgave.
Prosessen vil gå betydelig raskere hvis du øver mye. I fremtiden trenger du kanskje bare å se x- og y-aksene for å huske alt, eller du trenger kanskje ikke engang et diagram lenger.

Artikler om emnet "Lær enhetssirkelen utenat"

Lære noe utenat

Lær henry viiis koner utenat

Lær noe raskt utenat

Lær et essay utenat

Оцените, пожалуйста статью