Hvordan beregne summen av indre vinkler: 8 trinn (med bilder)

Innhold

Trinn
- Metode 1 av 2: Bruke formelen
- Metode 2 av 2: Tegn trekanter
Tips
Nødvendigheter

En polygon er en lukket figur med rette sider. Ved hvert toppunkt i en polygon er det både en indre og ytre vinkel, som tilsvarer de indre og ytre vinklene til den lukkede figuren. Å forstå sammenhengene mellom disse vinklene er nyttig i ulike geometriske problemer. Spesielt er det nyttig å vite hvordan man beregner summen av de indre vinklene i en polygon. Dette kan gjøres med en enkel formel eller ved å dele polygonet i trekanter.

Trinn

Metode 1 av 2: Bruke formelen

1. Skriv formelen for å finne summen av de indre vinklene. Formelen er

s du m = (n - 2) \times 180

$sum=(n-2) ganger 180$ , hvorved

s du m

$sum$ er summen av de indre vinklene til polygonet, og

n

$n$ er lik antall sider i polygonet.

Verdien 180 kommer fra antall grader i en trekant. Den andre delen av formelen, $n - 2$ $n-2$ er en måte å bestemme hvor mange trekanter polygonet kan deles inn i. Så formelen beregner i hovedsak antall grader i trekantene som utgjør polygonet.
Denne metoden fungerer uansett om du har å gjøre med en vanlig eller uregelmessig polygon. Regelmessige og uregelmessige polygoner med samme antall sider vil alltid ha samme sum av alle indre vinkler, den eneste forskjellen er at i en vanlig polygon har alle indre vinkler samme verdi. I en uregelmessig polygon vil noen vinkler være mindre, noen større, men de vil fortsatt summere seg til samme antall grader som i den vanlige formen.

Bilde med tittelen Beregn summen av indre vinkler Trinn 2

2. Tell antall sider i polygonet ditt. Husk at en polygon må ha minst tre rette sider.

For eksempel, hvis du vil finne summen av de indre vinklene til en sekskant, vil du telle seks sider.

Bilde med tittelen Beregn summen av indre vinkler Trinn 3

3. Behandle verdien for n{displaystyle n} $n$ i formelen. Husk at

n

$n$ antall sider i polygonet ditt er.

For eksempel, hvis du har å gjøre med en sekskant, da

n = 6

$n=6$ , fordi en sekskant har seks sider. Så formelen din vil se slik ut:

s du m = (6 - 2) \times 180

$sum=(6-2) ganger 180$

Bilde med tittelen Beregn summen av indre vinkler Trinn 4

4. Løs for n{displaystyle n} $n$ . For å gjøre dette, trekk to fra antall sider, og gang forskjellen med 180. Dette gir deg, i grader, summen av de indre vinklene i polygonet ditt.

For å finne summen av de indre vinklene til en sekskant, regn for eksempel:

s du m = (6 - 2) \times 180

$sum=(6-2) ganger 180$

s du m = (4) \times 180

$sum=(4) ganger 180$

s du m = (4) \times 180 = 720

$sum=(4) ganger 180=720$
Så summen av de indre vinklene til en sekskant er 720 grader.

Metode 2 av 2: Tegn trekanter

Bilde med tittelen Beregn summen av indre vinkler Trinn 5

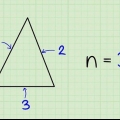
1. Tegn polygonen hvis vinkler du må legge til. Polygonen kan ha et hvilket som helst antall sider og kan være regelmessig eller uregelmessig.

For eksempel, hvis du trenger å finne summen av de indre vinklene til en sekskant, kan du tegne en sekskantet form.

Bilde med tittelen Beregn summen av indre vinkler Trinn 6

2. Velg ett toppunkt. Kall dette toppunktet A.

Et toppunkt er et punkt der to sider av en polygon møtes.

Bilde med tittelen Beregn summen av indre vinkler Trinn 7

3. Tegn en rett linje fra punkt A til toppunktet i polygonet. Linjene skal ikke krysse. Du skal lage noen trekanter.

Du trenger ikke å tegne linjer til de tilstøtende hjørnene, fordi de allerede er forbundet med en side.

For eksempel, for en sekskant, må du tegne tre linjer, dele formen i fire trekanter.

Bilde med tittelen Beregn summen av indre vinkler Trinn 8

4. Multipliser antall trekanter du har laget med 180. Siden det er 180 grader i en trekant, ved å multiplisere antall trekanter i polygonet ditt med 180, kan du finne summen av de indre vinklene til polygonet ditt.

Siden du delte sekskanten i fire trekanter, regner du

4 \times 180 = 720

$4 ganger 180=720$ og du får totalt 720 grader inne i polygonet.

Tips

Sjekk arbeidet ditt på papir ved å bruke en gradskive ved å legge til de innvendige vinklene manuelt. Vær forsiktig når du tegner sidene av polygonet, da de må være rette.