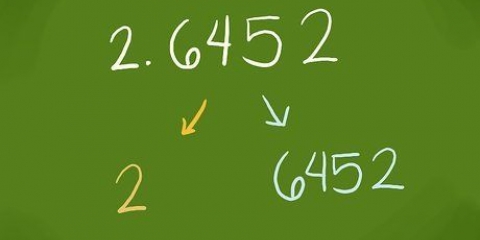I dette eksemplet er det første settet med tre tall multiplisert med 10. Bestem den største kuben som er mindre enn 10. Det er 8, og terningroten er 2. Skriv tallet 2 over det radikale tegnet, over tallet 10. Skriv ned verdien av  , lik 8, under tallet 10; tegne en linje og trekk fra tallene på samme måte som i lang divisjon. Resultatet er 2.
, lik 8, under tallet 10; tegne en linje og trekk fra tallene på samme måte som i lang divisjon. Resultatet er 2. Etter denne minussummen har du det første sifferet i svaret ditt. Du må sjekke om dette ene tallet er nøyaktig nok. I de fleste tilfeller vil dette ikke være tilfelle. Du kan sjekke dette ved å heve tallet til kuben og se om det er nærme nok ønsket resultat. I dette tilfellet  tilsvarer 8, og det er egentlig ikke i nærheten av 10, så du må gå videre.
tilsvarer 8, og det er egentlig ikke i nærheten av 10, så du må gå videre. 
Til venstre for den vertikale linjen, skriv ned løsningen av neste divisor, som summen av tre separate tall. Angi de tomme feltene for disse tallene ved å understreke tre mellomrom med plusstegn under dem. 


Beregn nå 3 ganger 10 ganger hvert av de to tallene som finnes i løsningen over radikalen. For dette enkle problemet betyr det 3*10*2*1, som er lik 60. Legg dette til de 1200 du allerede hadde, og du får 1260. Til slutt legger du til kvadratet til det siste sifferet. I dette eksemplet er det 1; og 1^2 er fortsatt 1. Så den totale divisor er 1200+60+1, eller 1261. Merk dette til venstre for den vertikale linjen. 

Du kan sjekke nøyaktigheten til dette resultatet ved å bruke kuben: 2.1*2.1*2.1. Resultatet er 9.261. Hvis du synes resultatet er nøyaktig nok, kan du stoppe. Vil du ha et mer eksakt svar, må du gjennom en ny runde. 
Ta den neste gruppen med tre tall ned. I dette tilfellet er dette tre nuller, som kommer etter resten 739 og dermed 739.000 former. Start divisor på 300 ganger kvadratet av tallet over radikalen. Dette er  , og derfor 132.300.
, og derfor 132.300. Velg neste siffer i løsningen din slik at du kan gange det med 132.300 og mindre fra 739.000 av resten. Et godt valg ville være 5, fordi 5*132.300=661.500. Skriv tallet 5 i neste mellomrom over den radikale linjen. Finn 3 ganger det forrige tallet over den radikale linjen, 21, ganger det siste sifferet du nettopp skrev ned, 5, ganger 10. Dette gir  .
. Til slutt kvadrerer du det siste sifferet. Dette er 
Legg til divisorens termer og du får 132.300+3150+25=135.475. 
Multipliser divisor med det siste sifferet i løsningen din. 135.475*5=677.375. trekke fra. 739.000-677.375=61.625. Vurder om løsning 2.15 er nøyaktig nok. Beregn kuben og du får  .
. 


I eksempeloppgaven faller 600 (målnummeret ditt) omtrent halvveis mellom grensetallene 512 og 729. Så velg din 5 som ditt neste tall. 
I dette eksemplet multipliserer du 

For eksempel, i dette problemet,  større enn målet (600). Så du reduserer anslaget til 8,4. Ta kuben av dette tallet og sammenlign det med målet ditt. du vil se det
større enn målet (600). Så du reduserer anslaget til 8,4. Ta kuben av dette tallet og sammenlign det med målet ditt. du vil se det  . Dette er nå lavere enn målet ditt. Dette forteller deg at kuberoten av 600 må være minst 8,4, men mindre enn 8,5.
. Dette er nå lavere enn målet ditt. Dette forteller deg at kuberoten av 600 må være minst 8,4, men mindre enn 8,5. 
I denne eksempeloppgaven viser den siste runden med beregninger det  , samtidig som
, samtidig som  . Målet (600) er litt nærmere 592 enn 614. Så anslår du neste tall litt mindre enn halvveis mellom 0 og 9. Et godt valg er 4, som vil gi deg et estimat på terningroten på 8,44.
. Målet (600) er litt nærmere 592 enn 614. Så anslår du neste tall litt mindre enn halvveis mellom 0 og 9. Et godt valg er 4, som vil gi deg et estimat på terningroten på 8,44. 
For dette eksempelproblemet, start med å merke det  . Dette er rett over målet, så slipp noen og test 8.43. Dette gir
. Dette er rett over målet, så slipp noen og test 8.43. Dette gir  som resultat. Så du vet at terningroten av 600 er litt mer enn 8,43 og litt mindre enn 8,44.
som resultat. Så du vet at terningroten av 600 er litt mer enn 8,43 og litt mindre enn 8,44. 
For eksempelet med terningsroten av 600, forutsatt to desimaltall, er 8,43 mindre enn 1 unna måltallet. Hvis du fortsetter til tre sifre etter desimaltegnet, vil du se det  hvis resultatet er 0,1 mindre enn det faktiske svaret.
hvis resultatet er 0,1 mindre enn det faktiske svaret. 

For å lære mer om Newtons binomiale og få dette resultatet, les mer om å multiplisere binomialer på wikiHow. Hvis du ønsker en mer dyptgående, rask versjon, les mer om Pascals trekant. 

Det første leddet inneholder et flertall på 1000. Du velger først et tall som kan heves til kuben og fortsatt holde seg innenfor rekkevidden til lang divisjon som det første sifferet. Dette gir begrepet 1000A^3 i binomialet. Det andre leddet i Newtons binomiale har en koeffisient på 300. (Dette er fra  .) Husk at når du beregner terningsroten, ble det første sifferet i hvert trinn multiplisert med 0300.
.) Husk at når du beregner terningsroten, ble det første sifferet i hvert trinn multiplisert med 0300. Det andre sifferet i hvert trinn i terningrotberegningen kommer fra det tredje leddet i Newtons binomiale. I Newtons binomiale ser du begrepet 30AB^2. Det siste sifferet i hvert trinn er begrepet B^3. 
Beregning av kuberøtter for hånd
Innhold
Ved å bruke en kalkulator, beregne terningsroten av et hvilket som helst tall, er det bare å trykke på noen få taster. Men kanskje du ikke har en kalkulator, eller du vil imponere vennene dine med evnen din til å beregne en terningrot direkte. Det er en metode som ser litt tøff ut ved første øyekast, men som fungerer veldig enkelt med litt øvelse. Det er nyttig å ha litt ferdigkunnskaper innen regneferdigheter og beregning av kubikktall.
Trinn
Del 1 av 3: Utarbeide en prøveoppgave

1. Forbered oppgaven. Å løse terningsroten til et tall vil se ut som å løse lang divisjon, med noen forskjeller her og der. Det første trinnet er å skrive ned problemet riktig.
- Skriv ned tallet du vil finne terningroten av. Skriv tallene i grupper på tre, der kommaet er utgangspunktet. I dette eksemplet skal du finne terningroten av 10. Skriv dette ned som 10 000 000. Nullene er nødvendige for nøyaktigheten av svaret.
- Tegn en radikal av kuben over tallet. Dette tjener samme formål som den lange delingslinjen. Den eneste forskjellen er formen på symbolet.
- Sett et komma over linjen, rett over desimaltegnet i det opprinnelige tallet.

2. Kjenn kubene til enhetene. Dette skal du bruke i dine beregninger. Det gjelder følgende tredjemakter:











3. Finn det første sifferet i svaret ditt. Velg et tall som til kuben gir størst mulig utfall som er mindre enn det første settet med tre tall.
 , lik 8, under tallet 10; tegne en linje og trekk fra tallene på samme måte som i lang divisjon. Resultatet er 2.
, lik 8, under tallet 10; tegne en linje og trekk fra tallene på samme måte som i lang divisjon. Resultatet er 2. tilsvarer 8, og det er egentlig ikke i nærheten av 10, så du må gå videre.
tilsvarer 8, og det er egentlig ikke i nærheten av 10, så du må gå videre.
4. Lag oppstillingen for neste siffer. Skriv den neste gruppen med tre tall i resten, og tegn en kort vertikal linje til venstre for det resulterende tallet. Dette vil være tallet vi bruker for å bestemme neste siffer i terningrotløsningen din. I dette eksemplet vil dette være 2000, som er opprettet fra resten av 2 av forrige minussum, med gruppen på tre nuller du tok ned.

5. Finn starten på neste divisor. For den første delen av divisor, skriv tre hundre ganger kvadratet av det som er over radikalen. I dette tilfellet er det 2; 2^2 er 4, og 4*300=1200. Så skriv 1200 på den første tomme plassen. Divisor for dette trinnet i løsningen kommer til å være 1200, pluss noe annet du skal beregne om et minutt.

6. Finn neste tall i terningroten din. Finn det neste sifferet i løsningen ved å velge det du kan multiplisere med divisor (1200-og-noe), og trekk fra resten av 2000. Dette kan bare være 1, fordi 2 ganger 1200 tilsvarer 2400, som er større enn 2000. Skriv tallet 1 i neste plass over radikalen.

7. Finn resten av divisoren. Divisoren i dette trinnet av løsningen består av tre deler. Den første delen er de 1200 du allerede har. Du må nå legge til to ekstra termer for å fullføre divisoren.

8. Multipliser og trekk fra. Rund denne delen av løsningen ved å multiplisere det siste sifferet i løsningen din - i dette tilfellet tallet 1 - ganger divisoren du nettopp regnet ut (1261). 1*1261 =1261. Skriv dette under 2000 og trekk 1261 fra det for å få 739.

9. Bestem deg for at du bør gå lenger for å få et mer nøyaktig svar. Etter å ha fullført minussummen for hvert trinn, må du sjekke om svaret ditt er nøyaktig nok. For terningroten av 10: etter den første minussummen var terningsroten bare 2, og det er egentlig ikke nøyaktig. Nå, etter andre runde, er løsningen 2,1.

10. Bestem dealeren for neste runde. I dette tilfellet, for mer trening og et mer presist svar, gjenta trinnene for en ny runde, som følger:
 , og derfor 132.300.
, og derfor 132.300. .
.

11. Multipliser divisor med resultatet. Etter å ha beregnet divisor i denne neste runden og utvidet løsningen med ett siffer til, fortsett som følger:
 .
.
12. Skriv ned det endelige svaret ditt. Resultatet over radikalen er kuberoten, med en nøyaktighet på tre signifikante sifre. I dette eksemplet er terningroten av 10 lik 2,15. Sjekk dette ved å beregne 2,15^3=9,94 som kan rundes opp til 10. Hvis du trenger et mer nøyaktig svar, fortsett til du er fornøyd.
Del 2 av 3: Finne terningroten gjennom gjentatt estimering

1. Bruk kubikktall for å angi øvre og nedre grenser. Når du blir bedt om en terningrot av et bestemt tall, start med å velge en terning som er så nærme som mulig uten å være større enn måltallet.
- For eksempel, hvis du vil finne terningroten av 600, husk (eller bruk en tabell med terninger) at
og
. Derfor vil løsningen på kuberoten av 600 være noe mellom 8 og 9. Bruk tallene 512 og 729 som øvre og nedre grenser for løsningen din.

2. Gjett neste tall. Du kjente det første sifferet på grunn av din kunnskap om visse kubikktall. For det neste sifferet, estimer et tall mellom 0 og 9 basert på hvor måltallet ditt faller mellom de to grensetallene.

3. Test gjetningen din ved å bestemme kuben. Prøv å multiplisere anslaget du jobber med nå for å se hvor nær du er måltallet.


4. Juster anslaget ditt der det er nødvendig. Etter å ha hevet til kuben for din siste gjetning, kontroller resultatet mot måltallet. Hvis resultatet er større enn målet, bør anslaget ditt være mindre. Hvis resultatet er mindre enn målet, må du justere det oppover til du når målet.
 større enn målet (600). Så du reduserer anslaget til 8,4. Ta kuben av dette tallet og sammenlign det med målet ditt. du vil se det
større enn målet (600). Så du reduserer anslaget til 8,4. Ta kuben av dette tallet og sammenlign det med målet ditt. du vil se det  . Dette er nå lavere enn målet ditt. Dette forteller deg at kuberoten av 600 må være minst 8,4, men mindre enn 8,5.
. Dette er nå lavere enn målet ditt. Dette forteller deg at kuberoten av 600 må være minst 8,4, men mindre enn 8,5.
5. Anslå neste tall for et mer nøyaktig svar. Fortsett denne prosedyren med å estimere tall fra 0 til 9, til svaret ditt er så nøyaktig som du vil at det skal være. For hver estimeringsrunde, start med å sjekke plasseringen av den siste beregningen mellom grensetallene.
 , samtidig som
, samtidig som  . Målet (600) er litt nærmere 592 enn 614. Så anslår du neste tall litt mindre enn halvveis mellom 0 og 9. Et godt valg er 4, som vil gi deg et estimat på terningroten på 8,44.
. Målet (600) er litt nærmere 592 enn 614. Så anslår du neste tall litt mindre enn halvveis mellom 0 og 9. Et godt valg er 4, som vil gi deg et estimat på terningroten på 8,44.
6. Fortsett å estimere og justere Gjør dette så mange ganger som nødvendig, hev anslaget til kuben og se hvordan det er sammenlignet med måltallet. Se etter tall som er like under eller like over måltallet.
 . Dette er rett over målet, så slipp noen og test 8.43. Dette gir
. Dette er rett over målet, så slipp noen og test 8.43. Dette gir  som resultat. Så du vet at terningroten av 600 er litt mer enn 8,43 og litt mindre enn 8,44.
som resultat. Så du vet at terningroten av 600 er litt mer enn 8,43 og litt mindre enn 8,44.
7. Fortsett til du når ønsket nøyaktighet. Fortsett å estimere, sammenligne og re-estimere, så lenge det er nødvendig, til løsningen din er så nøyaktig som du vil at den skal være. Merk at med hver desimal kommer måltallene dine nærmere og nærmere det faktiske tallet.
 hvis resultatet er 0,1 mindre enn det faktiske svaret.
hvis resultatet er 0,1 mindre enn det faktiske svaret.Del 3 av 3: Forstå hvordan denne beregningen fungerer

1. Gå over Newtons binomiale igjen. For å forstå hvorfor denne algoritmen fungerer for å bestemme kuberøtter, må du først tenke tilbake på hvordan kuben ser ut som binomial. Du har sannsynligvis lært dette i matematikk på videregående (og som de fleste har du sannsynligvis glemt det ganske raskt). Velg to variabler  og
og  for å representere enheter. Deretter regner du ut binomialet til
for å representere enheter. Deretter regner du ut binomialet til  for tiere.
for tiere.
 og
og  for å representere enheter. Deretter regner du ut binomialet til
for å representere enheter. Deretter regner du ut binomialet til  for tiere.
for tiere. - Bruk begrepet
å lage et dusin. Uansett hvilken karakter du velger
,
vil danne et dusin. For eksempel hvis
er 2 og
er 6, blir da
lik 26.

2. Skriv binomialet i en terning. Vi jobber nå bakover, ved først å bestemme kuben og deretter se hvorfor kuberøtterløsningen fungerer. Vi trenger verdiene til  finne. Dette gjør du ved å trene
finne. Dette gjør du ved å trene  . Dette er en for lang beregning til å vise her, men sluttresultatet er det
. Dette er en for lang beregning til å vise her, men sluttresultatet er det  .
.
 finne. Dette gjør du ved å trene
finne. Dette gjør du ved å trene  . Dette er en for lang beregning til å vise her, men sluttresultatet er det
. Dette er en for lang beregning til å vise her, men sluttresultatet er det  .
.
3. Kjenn betydningen av lang divisjon. Merk at metoden for å beregne terningsroten fungerer akkurat som lang divisjon. I lang divisjon ser du at to faktorer multiplisert sammen, gi tallet du startet med. I denne beregningen er tallet du leter etter (tallet som havner over radikalen) terningsroten. Det betyr at det er lik termen (10A+B). Selve A og B er irrelevante nå, så lenge du forstår forholdet til svaret.

4. Se den utvidede versjonen. Når du ser på Newtons binomiale, ser du hvorfor kuberotalgoritmen er riktig. Se hvordan divisor i hvert trinn i algoritmen er lik summen av de fire leddene du trenger for å beregne og legge sammen. Disse vilkårene oppstår som følger:
 .) Husk at når du beregner terningsroten, ble det første sifferet i hvert trinn multiplisert med 0300.
.) Husk at når du beregner terningsroten, ble det første sifferet i hvert trinn multiplisert med 0300.
5. Se nøyaktighet vokse. Når du trener lang divisjon, gir hvert trinn du fullfører stor nøyaktighet til svaret ditt. Eksempelproblemet som er utdypet i denne artikkelen er for eksempel for å bestemme kuberoten av 10. I det første trinnet er løsningen 2, fordi  kommer nærme, men er mindre enn 10. Faktisk,
kommer nærme, men er mindre enn 10. Faktisk,  . Etter andre runde er løsningen din 2.1. Når du har klart dette, får du det
. Etter andre runde er løsningen din 2.1. Når du har klart dette, får du det , og det er mye nærmere ønsket resultat (10). Etter tredje runde har du 2,15, og det gir deg
, og det er mye nærmere ønsket resultat (10). Etter tredje runde har du 2,15, og det gir deg  . Fortsett å jobbe i grupper på tre tall, så får du et så nøyaktig svar du ønsker.
. Fortsett å jobbe i grupper på tre tall, så får du et så nøyaktig svar du ønsker.
 kommer nærme, men er mindre enn 10. Faktisk,
kommer nærme, men er mindre enn 10. Faktisk,  . Etter andre runde er løsningen din 2.1. Når du har klart dette, får du det
. Etter andre runde er løsningen din 2.1. Når du har klart dette, får du det , og det er mye nærmere ønsket resultat (10). Etter tredje runde har du 2,15, og det gir deg
, og det er mye nærmere ønsket resultat (10). Etter tredje runde har du 2,15, og det gir deg  . Fortsett å jobbe i grupper på tre tall, så får du et så nøyaktig svar du ønsker.
. Fortsett å jobbe i grupper på tre tall, så får du et så nøyaktig svar du ønsker.Tips
- Som med alt vil dine matematiske ferdigheter forbedres med trening. Jo mer du øver, jo bedre vil du være i stand til å gjøre denne typen beregninger.
Advarsler
- Det er lett å ta feil her. Sjekk arbeidet ditt nøye og gå gjennom utdypningen på nytt.
Nødvendigheter
- Penn eller blyant
- Papir
- Hersker
- Viskelær
Artikler om emnet "Beregning av kuberøtter for hånd"
Оцените, пожалуйста статью
Populær