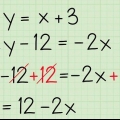Hvordan finne ut om to linjer er parallelle

Innhold

Trinn

Parallelle linjer er to linjer i et plan som aldri vil krysse hverandre (som betyr at de vil fortsette for alltid uten å berøre hverandre). En viktig egenskap ved parallelle linjer er at de har identiske skråninger. Helningen til en linje er definert som stigningen (endring i y-koordinater) over nedstigningen (endring i x-koordinater) av en linje, med andre ord hvor bratt linjen er. Parallelle linjer er ofte representert med to vertikale linjer (ll). For eksempel indikerer AB11CD at linjen AB er parallell med CD.

Trinn

Metode 1 av 3: Sammenligning av helningen til hver linje

1. Finn formelen for helningen. Helningen (hellingen) til en linje er definert av (Y₂ - Y₁)/(X₂ - X₁) hvor X og Y er de horisontale og vertikale koordinatene til punktene på linjen. Du må bestemme to punkter på linjen for å beregne denne formelen. Punktet nærmere bunnen av linjen er (X₁, Y₁) og punktet høyere opp på linjen, over det første punktet, er (X₂, Y₂).

Denne formelen kan omformuleres som økningen over avstanden. Det er den vertikale endringen sammenlignet med den horisontale endringen, eller linjens bratthet.
Hvis en linje peker til høyre og opp, vil den ha en positiv helning.
Hvis linjen peker til høyre og ned, vil den ha negativ helning.

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 2

2. Identifiser X- og Y-koordinatene til to punkter på hver linje. Et punkt på en linje er gitt av dens koordinat (X, Y) der X er plasseringen på den horisontale aksen og Y er plasseringen på den vertikale aksen. For å beregne stigningen må du bestemme to punkter på hver av de aktuelle linjene.

Poeng er enkle å bestemme hvis du har tegnet en linje på millimeterpapir.

For å bestemme et punkt, tegn en stiplet linje opp fra den horisontale aksen til den skjærer linjen. Posisjonen der du startet linjen på den horisontale aksen er x-koordinaten, mens y-koordinaten er der den stiplede linjen skjærer linjen på den vertikale aksen.

For eksempel: linje l har punktene (1, 5) og (-2, 4) mens linje r har punktene (3, 3) og (1, -4).

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 3

3. Bearbeid punktene for hver linje i helningsformelen. For å beregne stigningen, skriv inn tallene, trekk fra og del. Pass på at du setter inn koordinatene i riktig x- og y-verdi i formelen.

Til skråningen av linjen l å beregne: helning = (5 - (-4))/(1 - (-2))

Trekk fra: helning = 9/3

Del: helning = 3

Helningen på linjen r = (3 - (-4))/(3 - 1) = 7/2

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 4

4. Sammenlign bakkene til hver linje. Husk at to linjer kun er parallelle hvis de har samme helninger. Linjer kan virke parallelle på papiret og til og med være veldig nær parallelle, men hvis skråningene deres ikke er nøyaktig like, er de ikke parallelle.

I dette eksemplet er 3 ikke lik 7/2, så disse to linjene er ikke parallelle.

Metode 2 av 3: Bruke helnings- og skjæringsformelen

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 5

1. Finn formelen for helning og skjæringspunkt for en linje. Helningsformelen, ligningen til en rett linje. er y = mx + b, der m er helningen, b er skjæringspunktet med y-aksen, og x og y er variabler som representerer koordinater på linjen -- vanligvis ser du dem som x og y i ligningen. I dette skjemaet kan du enkelt bestemme helningen til linjen som variabelen `m`.

Et eksempel: omskriv 4y - 12x = 20 og y = 3x -1. Ligningen 4y - 12x = 20 må skrives om med algebra mens y = 3x -1 allerede har formen til helningsformelen og trenger ikke skrives om.

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 6

2. Omskriv formelen til linjen som helningsformel. Ofte vil formelen til linjen du får ikke være i form av et skråplan. Det tar bare litt matematikk og variabel omorganisering for å få den inn i hellingsformelen.

For eksempel: Omskriv linjen 4y-12x=20 som helningsformel.

Legg til 12x på begge sider av ligningen: 4y - 12x + 12x = 20 + 12x

Del hver side med 4 for å isolere y: 4y/4 = 12x/4 +20/4

Hellingsformel: y = 3x + 5

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 7

3. Sammenlign bakkene til hver linje. Husk at hvis to linjer er parallelle med hverandre, vil de ha nøyaktig samme helning. Ved å bruke ligningen y = mx + b, der m er helningen til linjen, kan du bestemme og sammenligne helningen til to linjer.

I vårt eksempel har den første linjen ligningen y = 3x + 5, så helningen er 3. Den andre linjen har en ligning på y = 3x - 1 som også har en helning på 3. Siden bakkene er identiske, er disse to linjene parallelle.

Merk at hvis disse ligningene har samme skjæringspunkt med y-aksen, vil de være samme linje i stedet for parallelle.

Metode 3 av 3: Bestemme en parallell linje med punkt-skråningsligningen

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 8

1. Definer punkt-helningsligningen. Med punkt-helningsligningen kan du skrive ligningen til en linje hvis du kjenner stigningen og har en (x, y) koordinat. Du bruker denne formelen hvis du vil definere en andre parallell linje på en allerede gitt linje med en viss helning. Formelen er y – y₁= m(x – x₁) hvor m er helningen til linjen, x₁ x-koordinaten til et gitt punkt på linjen og y₁ y-koordinaten til det punktet. Som i helningsformelen er x og y variabler som representerer koordinater på linjen -- vanligvis vil de forbli som x og y i ligningen.

Følgende trinn regner ut dette eksempelet: Skriv ligningen til en linje parallelt med linjen y = -4x + 3 som går gjennom punktet (1, -2).

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 9

2. Finn helningen til den første linjen. Når du skriver ligningen til en ny linje, må du først bestemme helningen til linjen som linjen må være parallell med. Pass på at ligningen til den opprinnelige linjen er en stigningsformel slik at du vet stigningen (m) med en gang.

Linjen vi ønsker å gjøre parallell er y = -4x + 3. I denne ligningen representerer -4 variabelen m og dermed helningen til linjen.

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 10

3. Identifiser et punkt på den nye linjen. Denne ligningen fungerer bare hvis du har en koordinat som går gjennom den nye linjen. Pass på at du ikke velger en koordinat som er på den opprinnelige linjen. Hvis de endelige ligningene dine har samme y-skjæringspunkt, er de ikke parallelle, men samme linje.

I vårt eksempel bruker vi koordinaten (1, -2).

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 11

4. Skriv ligningen til den nye linjen i punkt-hellingsformen. Husk at formelen er: y – y₁= m(x – x₁). Skriv inn helningen og koordinatene til punktet ditt for å gjøre ligningen til den nye linjen parallell med den første.

Ved å bruke vårt eksempel med helnings (m) -4 og (x, y) koordinater (1, -2) blir dette: y – (-2) = -4(x – 1)

Bilde med tittelen Finn ut om to linjer er parallelle Trinn 12

5. Forenkle ligningen. Etter at du har fylt inn tallene, kan ligningen forenkles til den mer vanlige helningsformelen. Linjen til denne ligningen, når den er tegnet i et koordinatsystem, er parallell med den gitte ligningen.

For eksempel: y - (-2) = -4(x - 1)

To negative gir en positiv: y + 2 = -4(x -1)

Bruk fordelingsegenskapen for å beregne -4(x -1): y + 2 = -4x + 4.

Trekk -2 fra begge sider: y + 2 - 2 = -4x + 4 - 2

Den forenklede ligningen: y = -4x + 2