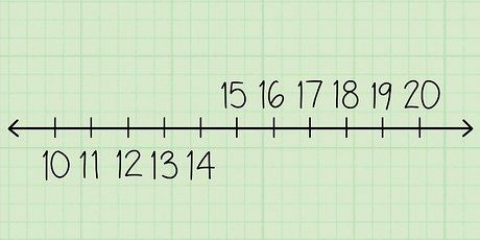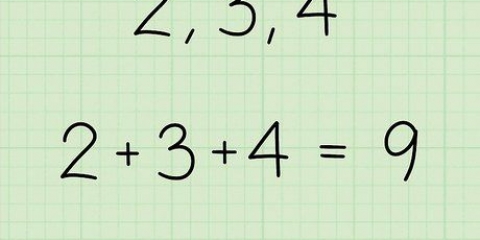Binær telling: 11 trinn (med bilder)

Innhold

Referansetabell
Trinn
- Metode 1 av 2: Lær binær telling
- Metode 2 av 2: Konverter fra binær til desimal
Tips

Vil du forbedre dine ferdigheter som nerd? Lær deretter tallsystemet slik datamaskiner bruker for å gjøre beregninger. Dette systemet kan se litt rart ut i begynnelsen, men du trenger bare noen få linjer og litt øvelse for å lære binær telling.

Referansetabell

Desimal	0	1	2	3	4	5	6	7	8	9	10
Binær	0	1	10	11	100	101	110	111	1000	1001	1010

Trinn

Metode 1 av 2: Lær binær telling

Bilde med tittelen Count in Binary Step 1

1. Lær hva binær betyr. Vårt vanlige tallsystem kalles desimal, med `grunntall ti`. Vi har ti forskjellige symboler for å skrive tall, fra 0 til 9. Binær er et "base to"-system, som bare bruker sifrene 0 og 1.

Bilde med tittelen Count in Binary Step 2

2. Legg til en ved å endre den siste 0-en til en 1. Hvis et binært tall ender på 0, kan du gå ett opp ved å endre 0 til en 1. Vi kan bruke dette til å telle de to første tallene, akkurat som du forventer:

0 = null

1 = en

For større tall kan du ignorere de forrige sifrene i nummeret. 1010 + 1 = 1011.

Bilde med tittelen Count in Binary Step 3

3. Skriv et annet tall hvis alle tallene er ett. Nå har vi en `1` for en, men det er ingen andre tall igjen! For å kunne telle til to nå, må vi skrive ned ett tall til. Plasser en `1` foran det første tallet, og `sett` alle andre sifre til 0.

0 = null

1 = en

10 = to

Dette er den samme regneregelen som vi bruker i desimalregning, når det ikke er andre sifre igjen (9 + 1 = 10). Dette er imidlertid mye mer vanlig i binær aritmetikk fordi det bare er to symboler.

Bilde med tittelen Count in Binary Step 4

4. Bruk disse reglene for å telle til fem. Disse reglene bringer deg til fem. Prøv å gjøre dette selv, og sjekk om du har forstått det riktig:

0 = null

1 = en

10 = to

11 = tre

100 = fire

101 = fem

Bilde med tittelen Count in Binary Step 5

5. Tell til seks. Nå løser vi fem pluss én, som er 101 + 1. Nøkkelen her er å ignorere det første sifferet. Bare legg til 1 + 1 på slutten for å få 10. (Slik skriver du tross alt `to`). Nå gjenoppretter vi det første sifferet og du får:

110 = seks

Bilde med tittelen Count in Binary Step 6

6. Tell til ti. Det er ingen nye regler å lære. Prøv det selv nå, og sjekk arbeidet ditt med denne listen:

110 = seks

111 = syv

1000 = åtte

1001 = ni

1010 = ti

Bilde med tittelen Count in Binary Step 7

7. Legg merke til når nye tall legges til. Ser du at tieren (1010) ikke ser ut som et `spesielt` binært tall? Åtte (1000) er mye viktigere, siden det tilsvarer 2 x 2 x 2. Fortsett å multiplisere med to for å finne de andre viktige tallene, for eksempel 16 (10000) og 32 (100000).

Bilde med tittelen Count in Binary Step 8

8. Øv med de større tallene. Nå vet du alt for å beregne med binære tall. Hvis du noen gang blir forvirret om hva det neste sifferet blir, er det bare å sjekke ut hva som skjedde med de forrige sifrene. Her er noen eksempler for å hjelpe deg:

Tolv pluss én = 1100 + 1 = 1101 (0 + 1 = 1, og de andre tallene forblir de samme).

Femten pluss én = 1111 + 1 = 10000 = seksten (Det er ikke flere nye symboler, så vi går tilbake til 0 og skriver en 1 i begynnelsen).

Førtifem pluss én = 101101 + 1 = 101110 = førtiseks (Vi vet at 01 + 1 = 10, og de andre tallene forblir de samme).

Metode 2 av 2: Konverter fra binær til desimal

Bilde med tittelen Count in Binary Step 9

1. Registrer verdien av hver binær posisjon. Når du lærte å telle i desimaler, lærte du også om `stedsverdiene`: enhetene, tiere og så videre. Siden binær har to symboler, multipliseres plassverdiene med to hver gang du flytter til venstre:

1 er enheten
10 er paret
100 er fireren
1000 er den åtte

Bilde med tittelen Count in Binary Step 10

2. Multipliser hvert siffer med plassverdien. Start med enheten helt til høyre og gang dette tallet (0 eller 1) med én. Bla til paret på en egen linje, og gang dette tallet med to. Gjenta dette mønsteret til du har multiplisert hvert siffer med plassverdien. Her er et eksempel:

Hva er det binære tallet 10011 i desimal?

Tallet helt til høyre er 1. Dette er enheten, så multipliser med én: 1 x 1 = 1.

Det neste tallet er også 1. Multipliser dette med to: 1 x 2 = 2.

Det neste sifferet er 0. Multipliser dette med fire: 0 x 4 = 0.

Det neste sifferet er også 0. Multipliser dette med åtte: 0 x 8 = 0.

Tallet lengst til venstre er 1. Multipliser dette med seksten (bak ganger to): 1 x 16 = 16.

Bilde med tittelen Count in Binary Step 11

3. Legg alle produktene sammen. Nå har du konvertert hvert siffer til dets desimalverdi. For å få den totale desimalverdien til det binære tallet, legg til alle desimalverdiene sammen. Her er resten av eksemplet:

1 + 2 + 16 = 19.

Det binære tallet 10011 er det samme som desimaltallet 19.