Slik beregner du omkretsen til en firkant

Innhold

Trinn

Omkretsen til en todimensjonal figur er den totale avstanden rundt figuren, eller summen av lengdene på sidene. Definisjonen av et kvadrat er en figur med fire like sider og fire rette vinkler (90°) mellom disse sidene. Siden alle sider har samme lengde, er det veldig enkelt å bestemme omkretsen til en firkant! Denne artikkelen dekker først hvordan du beregner omkretsen til et kvadrat hvis du vet lengden på en av sidene. Deretter viser vi deg hvordan du regner ut omkretsen hvis du bare kjenner arealet, og i den siste delen lærer vi deg hvordan du beregner omkretsen til et innskrevet kvadrat i en sirkel hvis radiuslengde er kjent.

Trinn

Metode 1 av 3: Finn omkretsen til en firkant hvis du vet lengden på en side

1. Tenk på formelen for omkretsen av et kvadrat. For et kvadrat hvor vi finner lengden på siden s omkretsen er bare fire ganger lengden på den siden: Omkrets = 4s (merk: i bildene brukes bokstaven P for omriss, fra den engelske `perimeter`).

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 2

2. Finn lengden på en side og gang den med 4 for å finne omkretsen. Avhengig av oppgaven må du kanskje måle med en linjal eller se på annen informasjon for å bestemme lengden på en side. Her er noen eksempler på omkretsberegninger:

Hvis kvadratet har en side med lengde 4:Omkrets = 4 * 4, med andre ord 16.

Hvis kvadratet har en side med lengde 6: Omkrets = 4 * 6, med andre ord 24.

Metode 2 av 3: Bestem omkretsen til et kvadrat hvis du kjenner området

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 3

1. Kjenn formelen for arealet til en firkant. Arealet til ethvert rektangel (husk at kvadrater er spesielle rektangler) kan defineres som basis ganger høyde.Siden grunnflate og høyde er like i tilfelle av en firkant, er arealet av en firkant med side s: s*s. Med andre ord: areal = s.

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 4

2. Ta kvadratroten av området. Kvadratroten av området gir deg lengden på en av sidene av kvadratet. For de fleste tall trenger du en kalkulator for å beregne kvadratroten. Skriv inn tallet først, og trykk deretter kvadratrottasten (√).

Hvis arealet av kvadratet er 20, så er lengden på siden s: =√20 eller 4.472

Hvis arealet av kvadratet er 25, så er lengden på siden s = √25 eller 5.

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 5

3. Multipliser lengden på siden med 4 for å finne omkretsen. Bruk sidelengdeverdien du nettopp fant i formelen Omkrets = 4s. Resultatet er omkretsen av kvadratet ditt!

For et kvadrat med et areal på 20 og en sidelengde på 4.473, er omkretsen: Omkrets = 4 * 4,472 eller 17.888.

For et kvadrat med et areal på 25 og en sidelengde på 5, er omkretsen: Omkrets = 4 * 5 eller 20.

Metode 3 av 3: Beregne omkretsen til et innskrevet kvadrat i en sirkel hvis du kjenner radiusen

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 6

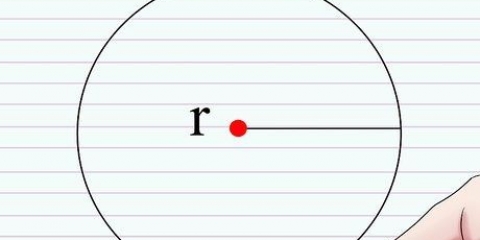
1. Forstå hva en innskrevet firkant er. En innskrevet firkant i en sirkel er en firkant tegnet i en sirkel med alle hjørner av firkanten i kontakt med sirkelen.

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 7

2. Forstå forholdet mellom radiusen til sirkelen og lengden på sidene i kvadratet. Avstanden fra midten av en innskrevet firkant til ethvert hjørne er lik radiusen til sirkelen. Til sidelengden s for å finne, må vi først forestille oss at vi kutter kvadratet i to diagonalt, slik at det dannes to likesidede trekanter. Disse trekantene har like sider en og b og en hypotenuse c, som vi vet er lik to ganger radiusen til sirkelen, dvs 2r.

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 8

3. Bruk Pythagoras teorem for å finne lengden på siden av firkanten. Pythagoras teorem er som følger: i en rettvinklet trekant er summen av kvadratene av lengdene til de rektangulære sidene (a,b) lik kvadratet av lengden på hypotenusen (c), a + b = c. Fordi sider en og b er like (vi har fortsatt å gjøre med en firkant!) og det vet vi c=2r vi kan nå skrive ut ligningen og forenkle den for å finne lengden på en side:

a + a = (2r), nå kan vi forenkle:

2a = 4(r), del nå begge sider med 2:

(a) = 2(r), ta nå kvadratroten av hver side:

a = √(2)r.Vår lengde på en side s av det innskrevne kvadratet = √(2)r.

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 9

4. Multipliser lengden på den ene siden av kvadratet med fire for å finne omkretsen. I dette tilfellet er omkretsen av kvadratet: Omkrets = 4√(2)r. Omkretsen til et innskrevet kvadrat i en sirkel er derfor alltid lik 4√(2)r, eller omtrent 5,657r

Bilde med tittelen Beregn omkretsen til en kvadrat Trinn 10

5. Løs et eksempelspørsmål. Vi tar et innskrevet kvadrat i en sirkel med en radius på 10. Det betyr at kvadratets diagonal = 2(10) eller 20. Pythagoras teorem lærer oss at: 2(a) = 20, Så 2a = 400. Del nå begge sider med to, vi ser det a = 200. Ta kvadratroten av hver side og vi ser det a = 14,142. Multipliser dette med 4 for å finne omkretsen av kvadratet ditt: Omkrets = 56,57.

Merk: du kunne også ha gjort det på denne måten: multipliser radiusen (10) med tallet 5 567. 10*5.567 = 56.57, men fordi det kan være vanskelig å huske, bør du gå gjennom hele prosessen.