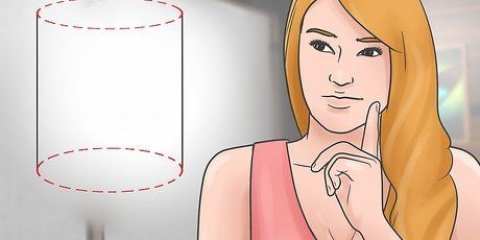
Radiusen (r) av en sirkel er avstanden fra ett punkt på sirkelen til sentrum av sirkelen. Diameteren (d) av en sirkel er avstanden fra ett punkt på sirkelen til et annet punkt rett overfor sirkelen, som går gjennom sentrum av sirkelen. Den greske bokstaven pi (π) står for forholdet mellom omkretsen delt på diameteren og er representert med tallet 3.14159265..., et irrasjonelt tall som verken har et siste siffer eller et gjenkjennelig mønster av repeterende sifre. Dette tallet rundes ofte av til 3,14 for standardberegninger. 
I de fleste matematikkoppgaver er radius eller diameter gitt. 
For eksempel: Hva er omkretsen til en sirkel med en radius på 3 cm? Skriv formelen: C = 2πr Fyll inn variablene: C = 2π3 Multipliser: C = (2*3*π) = 6π = 18,84 cm For eksempel: Hva er omkretsen til en sirkel med en diameter på 9 m? Skriv ned formelen: C = πd Fyll inn variablene: C = 9π Multipliser: C = (9*π) = 28,26 m 
Bestem omkretsen til en sirkel med en diameter på 5 m. C = πd = 5π = 15,7 m Bestem omkretsen til en sirkel med en radius på 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

Radiusen (r) av en sirkel er avstanden fra ett punkt på sirkelen til sentrum av sirkelen. Diameteren (d) av en sirkel er avstanden fra ett punkt på sirkelen til et annet punkt rett overfor sirkelen, som går gjennom sentrum av sirkelen. Den greske bokstaven pi (π) står for forholdet mellom omkretsen delt på diameteren og er representert med tallet 3.14159265..., et irrasjonelt tall som verken har et siste siffer eller et gjenkjennelig mønster av repeterende sifre. Dette tallet rundes vanligvis av til 3,14 for grunnleggende beregninger. 
I de fleste matematikkoppgaver er radius eller diameter gitt. 
For eksempel: hva er arealet av en sirkel med en radius på 3 m? Skriv formelen: A = r. Fyll inn variablene: A = π3. Kvaddra radiusen: r = 3 = 9 Multipliser med pi: en = 9π = 28,26 m For eksempel: hva er arealet av en sirkel med en diameter på 4 m? Skriv formelen: A = π(d/2). Fyll inn variablene: A = π(4/2). Del diameteren med 2: d/2 = 4/2 = 2 Kvaddra resultatet: 2 = 4 Multipliser med pi: en = 4π = 12,56 m 
Finn arealet av en sirkel med en diameter på 7 m. A = π(d/2) = π(7/2) = π(3,5) = 12,25 * π= 38,47 m. Finn arealet av en sirkel med en radius på 3 m. A = πr = π * 3 = 9 * π = 28,26 m 

For eksempel: beregn omkretsen til en sirkel med radius på (x + 1). Skriv formelen: C = 2πr Fyll inn den gitte informasjonen: C = 2π(x+1) 
For eksempel: beregn omkretsen til en sirkel med radius på (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Hvis verdien av `x` er gitt senere i oppgaven, kan du plugge den inn og få et helt tall. 
Finn arealet av en sirkel med en radius på 2x. A = πr = π(2x) = π4x = 12,56x Finn arealet av en sirkel med diameteren (x + 2). A = π(d/2) = π((x +2)/2) = ((x +2)/4)π
Beregne omkretsen og arealet til en sirkel
Innhold
Omkretsen (C) til en sirkel er dens omkrets, eller avstanden rundt den. Arealet (A) av en sirkel er hvor mye plass sirkelen opptar eller arealet som er omsluttet av sirkelen. Både areal og omkrets kan beregnes med enkle formler fra radiusen eller diameteren til sirkelen og verdien av pi.
Trinn
Del 1 av 3: Beregning av omkrets

1. Lær formelen for omkretsen av en sirkel. Det er to formler som kan brukes til å beregne omkretsen av en sirkel: C = 2πr eller C = d, hvor π er den matematiske konstanten og omtrent lik 3,14,r er lik radius og d lik diameteren.
- Siden radiusen til en sirkel er lik to ganger diameteren, er disse ligningene i hovedsak de samme.
- Enhetene for omkretsen kan være en hvilken som helst enhet for lengdemål: kilometer, meter, centimeter osv.

2. Forstå de ulike delene av formelen. Det er tre komponenter for å finne omkretsen til en sirkel: radius, diameter og π. Radius og diameter er relatert: radius er lik halve diameteren, mens diameteren er lik to ganger radius.

3. Mål radiusen eller diameteren til sirkelen. Plasser en linjal på den ene kanten av sirkelen, gjennom midten og til den andre siden av sirkelen. Avstanden fra sentrum av sirkelen er radius, mens avstanden fra den andre enden av sirkelen er diameteren.

4. Bearbeide og løse variablene. Når du har bestemt radiusen og/eller diameteren til sirkelen, kan du sette disse variablene inn i den riktige ligningen. Hvis du har bjelken, bruk C = 2πr, men hvis du vet diameteren så bruk C = d.

5. Øv med noen få eksempler. Nå som du har lært formelen, er det på tide å øve med noen eksempler. Jo flere problemer du løser, jo lettere blir det å løse dem i fremtiden.
Del 2 av 3: Beregning av areal

1. Lær formelen for arealet av en sirkel. Arealet av en sirkel kan beregnes ved å bruke enten dens diameter eller radius, med to forskjellige formler: A = r eller A = π(d/2), hvor π er den matematiske konstanten omtrent lik 3,14,r radiusen og d diameteren.
- Siden radiusen til en sirkel er lik halvparten av diameteren, er disse ligningene i hovedsak de samme.
- Enhetene for areal kan være en hvilken som helst enhet for lengde i annen: km i kvadrat (km), kvadrat meter (m), kvadratcentimeter (cm), etc.

2. Forstå de ulike delene av formelen. Det er tre komponenter for å finne omkretsen til en sirkel: radius, diameter og π. Radius og diameter er relatert til hverandre: radius er lik halve diameteren, mens diameteren er lik dobbel radius.

3. Mål radiusen eller diameteren til sirkelen. Plasser den ene enden av en linjal i et punkt på sirkelen, gjennom midten og til den andre siden av sirkelen. Avstanden fra sentrum av sirkelen er radius, mens avstanden fra det andre punktet på sirkelen er diameteren.

4. Fyll inn variablene og løs dem. Når du har bestemt radiusen og/eller diameteren til sirkelen, kan du plugge disse variablene inn i den riktige ligningen. Hvis du kjenner radiusen, bruk A = r, men hvis du vet diameteren så bruk A = π(d/2).

5. Øv med noen få eksempler. Nå som du har lært formelen, er det på tide å øve med noen eksempler. Jo flere problemer du løser, jo lettere blir det å løse andre problemer.
Del 3 av 3: Beregning av arealet og omkretsen med variabler

1. Bestem radien eller diameteren til sirkelen. Noen problemer gir en radius eller diameter med en variabel, for eksempel r = (x + 7) eller d = (x + 3). I dette tilfellet kan du fortsatt bestemme arealet eller omkretsen, men det endelige svaret ditt vil også inneholde den variabelen. Skriv ned radius eller diameter som angitt i uttalelsen.
- For eksempel: beregn omkretsen til en sirkel med radius på (x = 1).

2. Skriv formelen med den gitte informasjonen. Enten du vil beregne areal eller omkrets, følger du fortsatt de grunnleggende trinnene for å fylle inn det du vet. Skriv formelen for areal eller omkrets og fyll deretter inn de gitte variablene.

3. Løs oppgaven som om variabelen var et tall. På dette tidspunktet kan du bare løse problemet som du normalt ville gjort, og behandle variabelen som om den bare var et annet tall. Du trenger kanskje ved bruk av distribusjonsegenskap for å forenkle det endelige svaret.

4. Øv med noen eksempler. Nå som du har lært formelen, er det på tide å øve med noen eksempler. Jo flere problemer du løser, jo lettere blir det å løse nye.
Artikler om emnet "Beregne omkretsen og arealet til en sirkel"
Оцените, пожалуйста статью
Populær