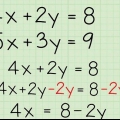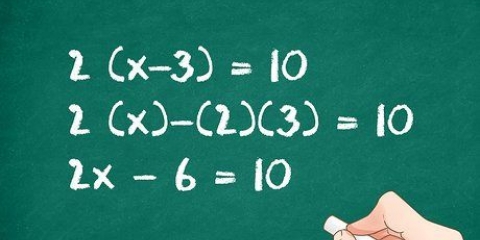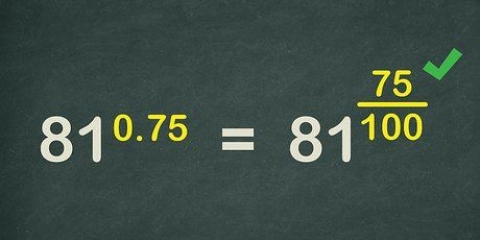Løse en kubikkligning

Innhold

Trinn

Første gang du kommer over en kubikkligning (av formen øks + bx + cx + d=0) det kan se nesten uløselig ut. Imidlertid har denne metoden for å løse kubiske ligninger eksistert i århundrer! Den ble oppdaget på 1500-tallet av de italienske matematikerne Niccolò Tartaglia og Gerolamo Cardano . Det var en av de første formlene som var ukjent for de gamle grekerne og romerne. Å løse kubikklikninger kan være veldig vanskelig, men med riktig tilnærming (og nok grunnleggende kunnskap) kan selv de vanskeligste kubikklikninger temmes.

Trinn

Metode 1 av 3: Løs det med abc-formelen

1. Sjekk om kubikkligningen inneholder en konstant. Som angitt ovenfor har kubiske ligninger formen øks + bx + cx + d=0. b, c, og d kan være 0 uten å endre om det er en kubikkligning eller ikke - betyr egentlig at en ligning ikke trenger å bestå av alle ledd bx, cx eller d å være en kubikkligning. Du begynner å bruke denne relativt enkle metoden for å løse kubiske ligninger ved først å sjekke om ligningen din har en konstant (a d-hvor i). Er dette ikke tilfelle, så kan du de abc formel å finne svarene på ligningen med litt matematikk.

Hvis ligningen inneholder en konstant, må du bruke en annen metode. Se nedenfor for alternative tilnærminger.

Bilde med tittelen Solve a Cubic Equation Step 2

2. løse opp en X ut av ligningen. Siden ligningen din ikke inneholder en konstant, har hvert ledd i ligningen en X-variabel. Dette betyr at a X kan tas ut av ligningen for å forenkle den. Gjør dette og skriv om ligningen din i skjemaet X(øks + bx + c).

Anta for eksempel at du har ligningen 3X + -2X + 14X=0. Av a X utenfor parentes, får vi X(3X + -2X + 14)=0.

Bilde med tittelen Løs en kubikkligning Trinn 3

3. Bruk abc-formelen til å løse begrepene i parentes. Du har kanskje lagt merke til at vilkårene for den nye ligningen din i parentes er i form av en kvadratisk ligning (øks + bx + c). Dette betyr at vi kan finne verdiene der andregradsligningen er lik null med a, b og c i abc-formelen ({-b +/-√ (b- 4ac)}/2en). Dette vil finne to av svarene til kubikkligningen din.

I vår eksempelutsagn fyller vi inn våre verdier a, b og c (henholdsvis 3, -2 og 14) i den andregradsligningen i:

{-b +/-√ (b- 4ac)}/2en

{-(-2) +/-√ ((-2)-4(3)(14))}/2(3)

{2 +/-√ (4 - (12)(14))}/6

{2 +/-√ (4 - (168)}/6

{2 +/-√ (-164)}/6

Svar 1:

{2 + √(-164)}/6

{2 + 12.8Jeg}/6

Svar 2:

{2–12.8Jeg}/6

Bilde med tittelen Løs en kubikkligning Trinn 4

4. Bruk null og kvadratisk svar som svar på kubikkligningen din. Firkantede ligninger har to løsninger, men kubiske ligninger har tre. Du har allerede to - dette er svarene du fant ved å regne ut "kvadratligningen" i parentes. I de tilfellene der en ligning er passende for denne "utenfor parentes", vil det tredje svaret alltid være 0 er. Gratulerer - du har nettopp løst en kubikkligning.

Grunnen til at dette fungerer har å gjøre med det grunnleggende faktum at ethvert tall multiplisert med null er lik null. Når du konverterer ligningen til formen X(øks + bx + c)=0, du deler i hovedsak de to i deler: en del er X-variabel utenfor parentes og den andre er kvadratet innenfor parentes. Hvis noen av disse delene er lik null, så er hele ligningen det også. Så hvis de to svarene til kvadratet innenfor parentesen gjør den delen til null, vil svarene på kubikkligningen også gjøre delen utenfor parentesen lik null.

Metode 2 av 3: Løsning ved hjelp av lister med faktorer

Bilde med tittelen Løs en kubikklikning Trinn 5

1. Sørg for at kubikkligningen din har en konstant. Selv om metoden ovenfor er nyttig fordi den ikke krever at du lærer nye matematiske ferdigheter, vil den ikke alltid fungere for å løse kubiske ligninger. Hvis ligningen din er i skjemaet øks + bx + cx + d=0 tilstand, og d er ikke-null, vil ikke parentesen fungere, og du trenger enten denne metoden eller den i neste del.

Anta for eksempel at du har den gitte ligningen 2X + 9X + 1. 3X=-6. I dette tilfellet vil en 0 til høyre for likhetstegnet kreve å legge til 6 på begge sider. Vår nye ligning er 2X + 9X + 1. 3X + 6=0, d=6, så vi kan ikke bruke parentesene fra forrige del.

Bilde med tittelen Løs en kubikklikning Trinn 6

2. Bestem faktorene til en og d. For å løse den kubiske ligningen, start med å bestemme faktorene til en (koeffisienten til X vilkår d (konstanten på slutten av ligningen). Som en påminnelse er faktorer de tallene som multiplisert sammen danner et annet tall. For eksempel fordi din 6 oppstår fra multiplikasjonen 6 &tid; 1 og 2 × 3, er 1, 2, 3 og 6 faktorer på 6.

I vårt eksempelutsagn, en=2 og d=6. Faktorene til 2 er 1 og 2. Faktorene på 6 er 1, 2, 3 og 6.

Bilde med tittelen Løs en kubikklikning Trinn 7

3. Del faktorene til en av faktorene til d. Nå lister du opp alle verdiene du får ved å dele hver faktor en av enhver faktor d. Dette resulterer vanligvis i mange brøker og noen få heltall. Heltallsløsningene til kubikkligningen din vil enten være ett av heltallene fra listen, eller det negative tallet til ett av disse tallene.

I ligningen vår beregner du faktorene til en (1, 2) på faktorene til d (1, 2, 3, 6) og du får følgende liste: 1, 1/2, 1/3, 1/6, 2 og 2/3. Nå legger vi til de negative tallene til listen for å gjøre den komplett: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 og -2/3. Heltallsløsningen til vår kubiske ligning finner du et sted i denne listen.

Bilde med tittelen Solve a Cubic Equation Step 8

4. Bruk syntetisk deling for å kontrollere svarene dine manuelt. Når du har kompilert listen over verdier, kan du finne heltallsløsningene til kubikkligningen din ved å raskt legge inn hvert heltall manuelt og sjekke hvilke som er lik null. Dersom du ikke ønsker å bruke tid på dette, finnes det en litt raskere metode iht en teknikk som kalles syntetisk deling. Hovedpoenget er at du deler heltall med originalen a, b, c og d koeffisientene til kubikkligningen din. Hvis du sitter igjen med en rest på 0, er verdien din en av løsningene til kubikkligningen.

Syntetisk deling er et komplekst emne - følg koblingen ovenfor for mer informasjon. Her er et eksempel på å finne en av løsningene på kubikkligningen vår ved hjelp av syntetisk divisjon:

-1 | 2 9 13 6

__| -2-7-6

__| 2 7 6 0

Siden vi ender opp med 0 som rest, vet vi at en av løsningene til vår kubikkligning er heltall -1 er.

Metode 3 av 3: Bruke "diskriminanten"

Bilde med tittelen Solve a Cubic Equation Step 9

1. Skriv ut verdiene til a, b, c og d. I denne metoden for å finne løsningene av en kubikkligning, vil vi stole sterkt på koeffisientene til leddene i ligningen vår. Av denne grunn er det lurt å bruke begrepene a, b, c og d skriv det ned før du starter slik at du ikke glemmer hva hver enkelt er.

For eksempel for sammenligningen X - 3X + 3X - 1, skriver vi en=1, b=-3, c=3 og d=-1. Ikke glem det av a X-variabel uten koeffisient antas det at koeffisienten er lik 1.

Bilde med tittelen Solve a Cubic Equation Step 10

2. Beregn Δ0=b - 3ac. Når du bruker diskriminanten til å løse kubikklikninger, trenger du litt mer avansert matematikk, men hvis du følger prosedyren nøye, vil du finne at den er et verdifullt verktøy for å løse de allerede vanskelige kubikklikningene. Start med å finne Δ0, den første av flere viktige verdier vi trenger, ved å erstatte de riktige verdiene i formelen b - 3ac.

I vårt eksempelproblem løser vi dette som følger:

b - 3ac

(-3) - 3(1)(3)

9 - 3(1)(3)

9 - 9=0=Δ0

Bilde med tittelen Solve a Cubic Equation Step 11

3. Regn ut Δ1=2b - 9ABC + 27end. Den neste viktige mengden vi trenger, Δ1, krever litt mer arbeid, men kan finnes på omtrent samme måte som Δ0. Bytt ut de riktige verdiene i formel 2b - 9ABC + 27end for verdien av Δ1.

I vårt eksempelproblem løser vi dette som følger:

2(-3) - 9(1)(-3)(3) + 27(1)(-1)

2(-27) - 9(-9) + 27(-1)

-54 + 81 - 27

81 - 81=0=Δ1

Bilde med tittelen Solve a Cubic Equation Step 12

4. Beregn Δ=Δ1 - 4Δ0) ÷ -27en. Så regner vi ut diskriminerende av kubikkligningen fra verdiene for Δ0 og Δ1. En diskriminant er ganske enkelt et tall som forteller oss noe om svarene til et polynom (ubevisst kan du allerede kjenner den kvadratiske diskriminanten: b - 4ac). Når det gjelder den kubiske ligningen, hvis diskriminanten er positiv, så har ligningen tre reelle løsninger. Hvis diskriminanten er null, har ligningen en eller to reelle løsninger, og noen av disse løsningene er delt. Hvis den er negativ, har ligningen bare én løsning. (En kubikkligning har alltid en reell løsning, fordi grafen alltid er minst én gang med X-aksekutt.)

I vårt eksempeloppgave er det veldig enkelt å bestemme Δ, fordi både Δ0 og Δ1=0. Vi løser dette på følgende måte:

Δ1 - 4Δ0) ÷ -27en

(0) - 4(0)) -27(1)

0 - 0 27

0=Δ, så ligningen vår har 1 eller 2 svar.

Bilde med tittelen Solve a Cubic Equation Step 13

5. regne ut C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). Den siste viktige verdien å beregne er C. Med denne viktige mengden kan vi endelig finne de tre løsningene. Løs dette som vanlig, bytt ut Δ1 og Δ0 der det er nødvendig.

I vårt eksempelproblem finner vi C følgende:

√(√((Δ1 - 4Δ0) + Δ1)/ 2)

√(√((0 - 4(0)) + (0))/ 2)

√(√((0 - 0) + (0))/ 2)

0=C

Bilde med tittelen Solve a Cubic Equation Step 14

6. Regn ut de tre svarene med variablene dine. Svarene på kubikkligningen din er gitt av formelen (b + uC + (Δ0/uC)) / 3en, hvorved du=(-1 + √(-3))/2 og n er 1, 2 eller 3. Skriv inn verdiene dine der det er nødvendig for å løse dette - dette krever mye matematikk, men bør gi deg tre mulige svar!

I vår eksempeloppgave kan vi løse dette ved å sjekke svaret når n er lik 1, 2 eller 3. Svarene vi får fra disse testene er de mulige svarene på vår kubikkligning - enhver løsning som gir 0 etter substitusjon i ligningen er riktig. Anta for eksempel at vi får 1 som svar på en av testene, fordi å skrive inn 1 i X - 3X + 3X - 1 resulterer i 0 hvis svar, da 1 et av svarene på vår kubikkligning.