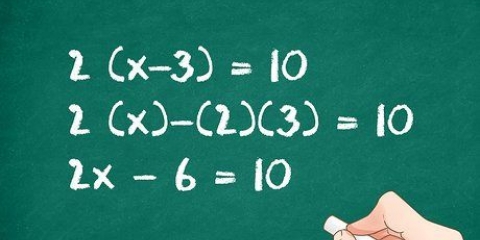Siden 3x har et begrenset antall mulige faktorer, 3x og x, kan du skrive disse i parentes: (3x +/- ? )(x +/-- ?) = 0. Bruk så en eliminasjonsmetode hvor du bruker faktorene 4 for å finne en kombinasjon som gir -11x som resultat av multiplikasjonen. Du kan bruke enten en kombinasjon av 4 og 1, eller 2 og 2, fordi multiplikasjonen av begge tallkombinasjonene gir 4. Husk at ett av begrepene må være negativt, fordi begrepet er -4. Prøv (3x +1)(x -4). Når du regner ut dette får du - 3x -12x +x -4. Kombinerer du begrepene -12x og x får du -11x, som er mellomleddet du ønsket å komme frem til. Nå har du faktorisert denne andregradsligningen. Et annet eksempel; vi prøver å faktorisere en ligning som ikke fungerer: (3x-2)(x+2) = 3x +6x -2x -4. Hvis du kombinerer disse begrepene, får du 3x -4x -4. Selv om produktet av -2 og 2 er lik -4, fungerer ikke mellomleddet fordi du lette etter -11x, ikke -4x. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Så begge løsningene fungerer hver for seg, og begge er bekreftet som fungerer og er korrekte i to forskjellige løsninger. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Løs kvadratiske ligninger
Innhold
En andregradsligning er en ligning der den største eksponenten til en variabel er to. Tre av de mest brukte metodene for å løse disse ligningene er: faktorisering, bruk av abc-formelen eller deling av kvadratet. Hvis du vil vite hvordan du mestrer disse metodene, følger du bare disse trinnene.
Trinn
Metode 1 av 3: Factoring

1. Flytt alle ledd til den ene siden av ligningen. Det første trinnet i faktorisering er å flytte alle ledd til den ene siden av ligningen, og la x være positiv. Bruk addisjons- eller subtraksjonsoperasjonen på leddene x, variabelen x og konstantene, flytt dem til den ene siden av ligningen på denne måten, og la ingenting stå igjen på den andre siden. Slik fungerer det:
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Faktor uttrykket. For å faktorisere uttrykket må du faktorisere faktorene til 3x, og faktorene til konstanten -4, for å multiplisere dem og deretter legge dem sammen for å gi verdien av mellomleddet, -11. Slik gjør du det:

3. Bestem at hvert par parenteser er lik null og behandle dem som separate ligninger. Dette får deg til å finne to verdier for x som begge gjør hele ligningen lik null. Nå som du har faktorisert ligningen, er det bare å gjøre hvert par parentes lik null. Så du kan skrive at: 3x +1 = 0 og x - 4 = 0.

4. Løs hver ligning. I en andregradsligning er det to gitte verdier for x. Løs hver ligning separat ved å isolere variabelen og skriv resultatene av x. Slik går det:

5. Sjekk x = -1/3 tommer (3x + 1)(x – 4) = 0:
Vi får (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... ved å erstatte:(-1 + 1)(-4 1/3) ?=? 0 ..... ved å forenkle:(0)(-4 1/3) = 0 ..... ved å multiplisere: så 0=0 ..... Ja, x = -1/3 fungerer
Vi får (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... ved å erstatte:(-1 + 1)(-4 1/3) ?=? 0 ..... ved å forenkle:(0)(-4 1/3) = 0 ..... ved å multiplisere: så 0=0 ..... Ja, x = -1/3 fungerer

6. Sjekk x = 4 tommer (3x + 1)(x - 4) = 0:
Vi får (3[4] + 1)([4] – 4) ?=? 0..... ved å erstatte:(13)(4 – 4) ?=? 0 ..... ved å dimme:(13)(0) = 0 ..... ved å multiplisere:0=0 ..... Ja, x = 4 fungerer
Vi får (3[4] + 1)([4] – 4) ?=? 0..... ved å erstatte:(13)(4 – 4) ?=? 0 ..... ved å dimme:(13)(0) = 0 ..... ved å multiplisere:0=0 ..... Ja, x = 4 fungerer
Metode 2 av 3: Bruk av Abc-formelen

1. Flytt alle ledd til den ene siden av ligningen og slå sammen de samme leddene. Flytt alle ledd til den ene siden av likhetstegnet, og hold leddet x positivt. Skriv begrepene i synkende størrelsesorden, så x kommer først etterfulgt av x, deretter konstanten. Slik gjør du det:
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Skriv ned abc-formelen. Dette er: {-b +/-√ (b - 4ac)}/2a

3. Bestem verdiene til a, b og c i andregradsligningen. Variabelen en er koeffisienten til x, b er koeffisienten til x og c er konstanten. For ligningen 3x -5x - 8 = 0, a = 3, b = -5 og c = -8. Skriv ned dette.

4. Bytt inn verdiene til a, b og c i ligningen. Nå som du kjenner verdiene til de tre variablene, kan du bare koble dem inn i ligningen som vi viser her:

5. Regne ut. Etter å ha fylt inn tallene løser du problemet videre. Nedenfor kan du lese hvordan det går videre:

6. Forenkle kvadratroten. Hvis tallet under det radikale tegnet er et perfekt kvadrat eller også et kvadrattall, får du et helt tall med kvadratroten. I andre tilfeller, forenkle kvadratroten så mye som mulig. Hvis tallet er negativt, og du er sikker på at dette er intensjonen, vil kvadratroten av tallet være mindre enkel. I dette eksemplet er √(121) = 11. Du kan da skrive at x =(5 +/- 11)/6.

7. Løs for positive og negative tall. Når du har kvittet deg med kvadratroten, kan du fortsette til du finner de negative og positive svarene for x. Nå som du har (5 +/- 11)/6, kan du skrive ned de to mulighetene:

8. Løs for de positive og negative svarene. Beregn videre:

9. Forenkle. For å forenkle, del svarene på det største tallet som er delelig med både telleren og nevneren. Så del den første brøken på 2 og den andre på 6 og du har løst x.
Metode 3 av 3: Deling av firkanten

1. Flytt alle leddene til den ene siden av ligningen. Sørg for at en av x er positivt. Slik gjør du det:
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- I denne ligningen, en lik 2, b er -12, og c er -9.

2. Flytt konstanten c til den andre siden. Konstanten er den numeriske verdien uten variabel. Flytt den til høyre side av ligningen:

3. Del de to sidene med koeffisienten til en eller x term. Hvis x ikke har noe ledd foran seg og har en koeffisient med verdien 1, kan du hoppe over dette trinnet. I dette tilfellet må du dele alle ledd med 2, slik:

4. Del b med to, kvadrater det og legg til resultatene på begge sider av er-tegnet.Deb i dette eksemplet er -6. Slik gjør du dette:

5. Forenkle begge sider. Faktor vilkårene til venstre for å få (x-3)(x-3), eller (x-3). Legg til vilkårene til høyre for å få 9/2 + 9, eller 9/2 + 18/2, som tilsvarer 27/2.

6. Finn kvadratroten av begge sider. Kvadratroten av (x-3) er ganske enkelt (x-3). Du kan også skrive kvadratroten av 27/2 som ±√(27/2). Derfor er x - 3 = ±√(27/2).

7. Forenkle kvadratroten og løs for x. For å forenkle ±√(27/2), se etter et perfekt kvadrat eller kvadrattall med tallene 27 eller 2 eller i faktorene deres. Kvadratnummeret 9 kan finnes i 27, fordi 9 x 3 = 27. For å eliminere 9 fra roten, skriv den som en egen rot og forenkle til 3, kvadratroten av 9. La √3 stå i telleren til brøken fordi den ikke kan skilles som en faktor fra 27, og gjør 2 til nevneren. Flytt så konstanten 3 fra venstre side av ligningen til høyre side og skriv ned de to løsningene for x:
Tips
- Som du kan se, har det radikale tegnet ikke helt forsvunnet. Derfor slås ikke begrepene i telleren sammen (de er ikke like vilkår). Så det er meningsløst å dele opp minuser og plusser. I stedet, ved å dele, sørger vi for at hver felles faktor forsvinner – men "KUN" hvis faktoren er lik for begge konstantene, "OG" koeffisienten til kvadratroten.
Artikler om emnet "Løs kvadratiske ligninger"
Оцените, пожалуйста статью
Populær