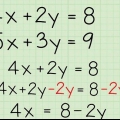2x - 2x = 0 4y - 2y = 2y 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2y = 6 Del 2y og 6 med 2 og få y = 3 
Sett inn y = 3 i ligningen 2x + 2y = 2 og løs for x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Du har løst likningssystemet ved subtraksjon. (x, y) = (-2, 3) 
Fyll inn (-2, 3) for (x, y) i ligningen 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Fyll inn (-2, 3) for (x, y) i ligningen 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6y + -6y = 0 8 + 4 = 12 Hvis du kombinerer dette får du et nytt produkt: 3x + 6y = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Del 4x og 12 med 3 for å få x = 3 
Plugg x = 3 inn i ligningen x - 6y = 4 for å finne y. 3 - 6 år = 4 -6y = 1 Del -6y og 1 med -6 for å få y = -1/6. Du har løst likningssystemet med addisjon. (x, y) = (3, -1/6) 
Fyll inn (3, -1/6) for (x, y) i ligningen 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Fyll inn (3, -1/6) for (x, y) i ligningen x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2y = 4 
3x + 2y = 10 + 4x - 2y = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Du har løst likningssystemet ved hjelp av multiplikasjon. (x, y) = (2, 2) 
Fyll inn (2, 2) for (x, y) i ligningen 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Fyll inn (2, 2) for (x, y) i ligningen 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4y --> 2x + 3y = 9 2(2 - 4y) + 3y = 9 4 - 8 år + 3 år = 9 4 - 5 år = 9 -5y = 9 - 4 -5y = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4y x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Du løste likningssystemet ved å bruke substitusjon. (x, y) = (6, -1) 
Fyll inn (6, -1) for (x, y) i ligningen 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Fyll inn (6, -1) for (x, y) i ligningen x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Løse et ligningssystem
Innhold
Å løse et ligningssystem krever å finne verdien av flere variabler i flere ligninger. Du kan løse et likningssystem ved hjelp av addisjon, subtraksjon, multiplikasjon eller substitusjon. Hvis du vil lære hvordan du løser et ligningssystem, er alt du trenger å gjøre å følge disse trinnene.
Trinn
Metode 1 av 4: Løs ved subtraksjon

1. Skriv den ene ligningen over den andre. Å løse disse likningene med subtraksjon er en ideell metode hvis du ser at begge likningene har samme variabel med samme koeffisient og fortegn. For eksempel, hvis begge ligningene har variabelen -2x, kan du bruke subtraksjon for å finne verdien av begge variablene.
- Skriv en likning over den andre slik at x- og y-variablene til begge likningene og tallene er under hverandre. Plasser minustegnet ved siden av det nederste tallet.
- For eksempel: Hvis du har følgende to ligninger: 2x + 4y = 8 og 2x + 2y = 2, vil det se slik ut:
- 2x + 4y = 8
- -(2x + 2y = 2)

2. Trekk fra lignende termer. Nå som de to ligningene er justert, er alt du trenger å gjøre å trekke fra de samme leddene. Gjør dette med ett termin om gangen:

3. Løs for gjenværende termin. Fjern enhver null fra ligningen som er opprettet, den endrer ikke verdien, og løs den gjenværende ligningen.

4. Skriv inn funnverdien til variabelen i en av ligningene. Nå som du vet at y = 3, kan du plugge denne verdien inn i den opprinnelige ligningen for å løse for x. Uansett hvilken ligning du velger, er svaret det samme. Så bruk den enkleste ligningen!

5. Sjekk svaret ditt. For å være sikker på at svaret er riktig, skriv inn begge svarene i begge ligningene. Slik gjør du det:
Metode 2 av 4: Løs ved addisjon

1. Skriv den ene ligningen over den andre. Å løse et likningssystem ved addisjon er den beste metoden, hvis du legger merke til at begge likningene har en variabel med samme koeffisient, men med forskjellig fortegn; for eksempel hvis en ligning inneholder variabelen 3x og den andre variabelen -3x.
- Skriv en likning over den andre slik at x- og y-variablene til begge likningene og tallene er under hverandre. Plasser plusstegnet ved siden av det nederste tallet.
- For eksempel: Du har følgende to ligninger 3x + 6y = 8 og x - 6y = 4, og skriv deretter den første ligningen over den andre som vist nedenfor:
- 3x + 6y = 8
- +(x - 6y = 4)

2. Legg til lignende termer sammen. Nå som de to ligningene er justert over hverandre, er alt du trenger å gjøre å legge til begrepene med samme variabel sammen:

3. Løs for gjenværende termin. Fjern eventuell null fra ligningen som har oppstått, den endrer ikke verdien. Løs den gjenværende ligningen.

4. Skriv inn funnverdien til denne variabelen i en av ligningene. Nå som du vet at x = 3, kan du koble denne verdien inn i den opprinnelige ligningen for å løse for y. Uansett hvilken ligning du velger, er svaret det samme. Så bruk den enkleste ligningen!

5. Sjekk svaret ditt. For å være sikker på at svaret er riktig, skriv inn begge svarene i begge ligningene. Slik gjør du det:
Metode 3 av 4: Løs ved multiplikasjon

1. Skriv den ene ligningen over den andre. Skriv en likning over den andre slik at x- og y-variablene til begge likningene og tallene er under hverandre. Hvis du bruker multiplikasjon, gjør du det fordi ingen av variablene har like koeffisienter - akkurat nå.
- 3x + 2y = 10
- 2x - y = 2

2. Sørg for like koeffisienter. Deretter multipliser en eller begge ligningene med et tall, slik at en av variablene har samme koeffisient. I dette tilfellet kan du multiplisere hele den andre ligningen med 2 slik at -y er lik -2y og dermed den første y-koeffisienten. Slik gjør du det:

3. Legg til eller trekk fra likningene. Nå er alt du trenger å gjøre å eliminere like vilkår ved å legge til eller trekke fra. Siden du har å gjøre med 2y og -2y her, er det fornuftig å bruke addisjonsmetoden fordi den er lik 0. Hvis du har å gjøre med 2y + 2y, bruk subtraksjonsmetoden. Her er et eksempel på hvordan du bruker addisjonsmetoden for å eliminere variabler:

4. Løs dette for gjenværende periode. Dette løses enkelt ved å finne verdien av begrepet som du ennå ikke har eliminert. Hvis 7x = 14, så er x = 2.

5. Skriv inn den funnet verdien i en av ligningene. Skriv inn leddet i en av de opprinnelige ligningene for å løse det andre leddet. Velg den enkleste ligningen for dette, dette er den raskeste.

6. Sjekk svaret ditt. For å være sikker på at svaret er riktig, skriv inn begge svarene i begge ligningene. Slik gjør du det:
Metode 4 av 4: Løs ved substitusjon

1. Isoler en variabel. Substitusjon er ideell når en av koeffisientene i en av ligningene er lik 1. Så er alt du trenger å gjøre å isolere denne variabelen til den ene siden av ligningen for å finne verdien.
- Hvis du jobber med ligningene 2x + 3y = 9 og x + 4y = 2, må du isolere x i den andre ligningen.
- x + 4y = 2
- x = 2 - 4y

2. Fyll inn verdien til variabelen du isolerte i den andre ligningen. Ta verdien av den isolerte variabelen og plugg den inn i den andre ligningen. Selvfølgelig ikke i samme ligning ellers løser du ingenting. Her er et eksempel på hvordan du gjør det:

3. Løs for den gjenværende variabelen. Nå som du vet at y = - 1, plugg denne verdien inn i den enklere ligningen for å finne verdien av x. Her er et eksempel på hvordan du gjør det:

4. Sjekk svaret ditt. For å være sikker på at svaret er riktig, skriv inn begge svarene i begge ligningene. Slik gjør du det:
Tips
- Du skal nå kunne løse et hvilket som helst lineært ligningssystem ved hjelp av addisjon, subtraksjon, multiplikasjon eller substitusjon, men én metode er vanligvis den mest passende avhengig av ligningene.
Artikler om emnet "Løse et ligningssystem"
Оцените, пожалуйста статью
Populær