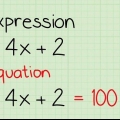Hvordan løse ligningssystemer ved å bruke to variabler

Innhold

Trinn
Tips
Advarsler

I et `ligningssystem` blir du bedt om å løse to eller flere ligninger samtidig. Når disse to inneholder forskjellige variabler, som x og y, eller a og b, kan det ved første øyekast være vanskelig å se hvordan man løser dem. Heldigvis, når du vet hva du skal gjøre, trenger du bare noen grunnleggende matematiske ferdigheter (og noen ganger litt kunnskap om brøker) for å løse problemet. Hvis det er nødvendig, eller hvis du er en visuell elev, kan du også lære hvordan du tegner likningene. Å tegne (plotte) en graf kan være nyttig for å "se hva som skjer", eller for å sjekke arbeidet ditt, men det kan også være tregere enn de andre metodene og vil ikke fungere med alle ligningssystemer.

Trinn

Metode 1 av 3: Bruke substitusjonsmetoden

1. Flytt variablene til forskjellige sider av ligningen. Denne `substitusjonsmetoden` starter med å `løse for x` (eller en hvilken som helst annen variabel) i en av ligningene. For eksempel har vi følgende ligninger: 4x + 2y = 8 og 5x + 3x = 9. La oss først se på den første ligningen. Omorganiser ved å trekke fra 2y fra hver side, og du får: 4x = 8 - 2y.

Denne metoden bruker ofte fraksjoner på et senere tidspunkt. Du kan også bruke elimineringsmetoden nedenfor, hvis du foretrekker å ikke jobbe med brøker.

Bilde med tittelen Løs systemer av algebraiske ligninger som inneholder to variabler Trinn 2

2. Del begge sider av ligningen for å `løse for x`. Når du har begrepet x (eller hvilken variabel du bruker) på den ene siden av ligningen, deler du begge sider av ligningen for å isolere variabelen. For eksempel:

4x = 8 - 2y

(4x)/4 = (8/4) - (2y/4)

x = 2 - y

Bilde med tittelen Løs systemer av algebraiske ligninger som inneholder to variabler Trinn 3

3. Koble dette tilbake til den andre ligningen. Sørg for å gå tilbake til Andre sammenligning, ikke den du allerede har brukt. I den ligningen erstatter du variabelen du løste slik at bare én variabel er igjen. For eksempel:

Du vet nå at: x = 2 - y.

Den andre ligningen, som du ikke har endret ennå, er: 5x + 3x = 9.

I den andre ligningen erstatter du x med `2 - ½y`: 5(2 - ½y) + 3y = 9.

Bilde med tittelen Løs systemer av algebraiske ligninger som inneholder to variabler Trinn 4

4. Løs for den gjenværende variabelen. Du har nå en ligning med bare én variabel. Bruk vanlige algebrateknikker for å løse den variabelen. Hvis variablene kansellerer hverandre, fortsett til siste trinn. Ellers vil du ende opp med et svar på en av variablene dine:

5(2 - ½y) + 3y = 9

10 – (5/2)y + 3y = 9

10 – (5/2)y + (6/2)y = 9 (Hvis du ikke forstår dette trinnet, lær hvordan legge til brøker. Dette er ofte, men ikke alltid, nødvendig med denne metoden).

10 + y = 9

y = -1

y = -2

Bilde med tittelen Løs systemer av algebraiske ligninger som inneholder to variabler Trinn 5

5. Bruk svaret til å løse den andre variabelen. Ikke gjør den feilen å fullføre problemet halvveis. Du må skrive inn svaret du fikk på nytt i en av de opprinnelige ligningene, slik at du kan løse den andre variabelen:

Du vet nå at: y = -2

En av de opprinnelige ligningene er: 4x + 2y = 8. (Begge ligningene kan brukes for dette trinnet).

Plugg inn -2 i stedet for y: 4x + 2(-2) = 8.

4x - 4 = 8

4x = 12

x = 3

Bilde med tittelen Løs systemer av algebraiske ligninger som inneholder to variabler Trinn 6

6. Vit hva du skal gjøre når begge variablene kansellerer hverandre. Når du x = 3y + 2 eller får et lignende svar i den andre ligningen, så prøver du å få en ligning med bare én variabel. Noen ganger ender du opp med en ligning i stedet uten variabler. Dobbeltsjekk arbeidet ditt, og sørg for å erstatte den (omorganiserte) første ligningen med den andre ligningen, ikke den første ligningen. Når du er sikker på at du ikke har gjort noen feil, får du ett av følgende resultater:

Hvis du ender opp med en ligning uten variabler og som ikke er sann (for eksempel 3 = 5), så har problemet ingen løsning. (Hvis du har tegnet likningene, vil du se at de er parallelle og aldri skjærer hverandre).

Hvis du ender opp med en ligning uten variabler, men de vi vil er sant (for eksempel 3 = 3), så har problemet et uendelig antall løsninger. De to ligningene er nøyaktig like hverandre. (Hvis du tegner de to likningene, vil du se at de overlapper nøyaktig).

Metode 2 av 3: Bruke eliminasjonsmetoden

1. Bestemmer variabelen som skal elimineres. Noen ganger vil ligningene "eliminere" hverandre i en variabel så snart du legger dem sammen. For eksempel når du gjør ligningene 3x + 2y = 11 og 5x - 2y = 13 kombinerer, vil `+2y` og `-2y` eliminere hverandre, med alle `ys fjernes fra ligningen. Se på ligningene i oppgaven din for å finne ut om noen av variablene vil bli eliminert på denne måten. Hvis ingen av variablene er eliminert, les videre til neste trinn for råd.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 7

Bilde med tittelen Løs systemer av algebraiske ligninger som inneholder to variabler Trinn 8

2. Multipliser en ligning for å eliminere en variabel. (Hopp over dette trinnet hvis variablene allerede har eliminert hverandre). Hvis ingen av variablene i ligningene elimineres av seg selv, må du endre en av ligningene slik at de gjør det. Dette er lettest å forstå med et eksempel:

Anta at du har ligningssystemet 3x - y = 3 og -x + 2y = 4.

La oss modifisere den første ligningen slik at variabelen y blir eliminert. (Du kan også gjøre dette for X gjør og få det samme svaret).

De - y` av den første ligningen bør elimineres med+ 2 år ` i den andre ligningen. Vi kan gjøre dette ved å - y å gange med 2.

Vi multipliserer begge sider av den første ligningen med 2, som følger: 2(3x - y)=2(3), og dermed 6x - 2y = 6. Nå vil - 2 år falle bort mot +2 år i den andre ligningen.

Bilde med tittelen Løs systemer av algebraiske ligninger som inneholder to variabler Trinn 9

3. Kombiner de to ligningene. For å kombinere to ligninger legger du sammen venstre og høyre side. Hvis du skrev ligningen riktig, bør en av variablene oppheve mot den andre. Her er et eksempel som bruker de samme ligningene som det siste trinnet:

Dine ligninger er: 6x - 2y = 6 og -x + 2y = 4.

Kombiner venstre side: 6x - 2y - x + 2y = ?

Kombiner høyresidene: 6x - 2y - x + 2y = 6 + 4.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 10

4. Løs for den siste variabelen. Forenkle den kombinerte ligningen, og bruk deretter grunnleggende algebra for å løse den siste variabelen. Hvis det ikke er noen variabler igjen etter forenkling, hopp til siste trinn i denne delen. Ellers bør du ende opp med et enkelt svar på en av variablene dine. For eksempel:

Du har: 6x - 2y - x + 2y = 6 + 4.

Grupper variablene X og y med hverandre: 6x - x - 2y + 2y = 6 + 4.

Forenkle: 5x = 10

Løs for x: (5x)/5 = 10/5, så det x = 2.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 11

5. Løs for de andre variablene. Du har funnet én variabel, men du er ikke helt ferdig ennå. Bytt inn svaret ditt i en av de opprinnelige ligningene slik at du kan løse den andre variabelen. For eksempel:

Du vet det x = 2, og den av dine originale ligninger 3x - y = 3 er.

Plugg inn 2, i stedet for x: 3(2) - y = 3.

Løs for y i ligningen: 6 - y = 3

6 - y + y = 3 + y, så 6 = 3 + år

3 = y

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 12

6. Vit hva du skal gjøre hvis begge variablene kansellerer hverandre. Noen ganger resulterer det å kombinere to ligninger i en ligning som ikke gir mening, eller som ikke hjelper deg med å løse problemet. Dobbeltsjekk arbeidet ditt fra starten, men hvis du ikke gjorde en feil, skriv ett av følgende svar:

Hvis den kombinerte ligningen din ikke har noen variabler og ikke er sann (som 2 = 7), så er det ingen løsning som gjelder for begge ligningene. (Hvis du tegner begge likningene, vil du se at de er parallelle og aldri skjærer hverandre).

Hvis den kombinerte ligningen din ikke har noen variabler og er sann (som 0 = 0), så er det et uendelig antall løsninger. De to ligningene er faktisk identiske. (Hvis du legger disse på en graf, vil du se at de overlapper hverandre fullstendig).

Metode 3 av 3: Tegne likningene

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 13

1. Bruk bare denne metoden når spesifisert. Med mindre du bruker en datamaskin eller en grafisk kalkulator, kan mange ligningssystemer bare løses tilnærmet ved å bruke denne metoden. Læreren eller matteboken din kan be deg om å bruke denne metoden, så du er sannsynligvis kjent med grafiske ligninger som linjer. Du kan også bruke denne metoden til å sjekke om svarene dine fra en av de andre metodene er riktige.

Den grunnleggende ideen er at du tegner begge likningene og bestemmer punktet der de skjærer hverandre. x- og y-verdiene på dette tidspunktet gir verdien av x og verdien av y i ligningssystemet.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 14

2. Løs begge likningene for y. Hold de to likningene adskilt, bruk algebra til å konvertere hver likning til formen `y = __x + __`. For eksempel:

Den første ligningen er: 2x + y = 5. Endre dette til: y = -2x + 5.

Den andre ligningen er: -3x + 6y = 0. Endre dette til 6y = 3x + 0, og forenkle tily = ½x + 0.

Er begge ligningene identiske, da blir hele linjen et "kryss". Skrive: uendelige løsninger.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 15

3. Tegn et koordinatsystem. Tegn en vertikal "y-akse" og en horisontal "x-akse" på et stykke millimeterpapir. Start på punktet der linjene krysser hverandre, og merk tallene 1, 2, 3, 4 osv. opp langs y-aksen og til høyre igjen langs x-aksen. Merk tallene -1, -2 osv. nedover y-aksen og til venstre langs x-aksen.

Hvis du ikke har millimeterpapir, bruk en linjal for å sørge for at tallene er jevnt fordelt.

Hvis du bruker store tall eller desimaler, må du kanskje skalere diagrammet. (For eksempel 10, 20, 30 eller 0.1, 0.2.0.3 i stedet for 1, 2, 3).

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 16

4. Tegn y-skjæringspunktet for hver linje. Når du har en ligning i skjemaet y = __x + __ du kan begynne å tegne grafen ved å tegne et punkt der linjen avskjærer y-aksen. Dette er alltid på en y-verdi, lik det siste tallet i denne ligningen.

I de nevnte eksemplene, én linje (y = -2x + 5) i y-aksen 5. Den andre linjen (y = ½x + 0) går gjennom nullpunktet 0. (Dette er punktene (0,5) og (0,0) i grafen).

Merk hver av linjene med en annen farge, hvis mulig.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 17

5. Bruk skråningen til å fortsette å tegne linjene. I skjemaet y = __x + __, er tallet for x de skråningen utenfor linjen. Hver gang x økes med én, vil y-verdien øke med verdien av helningen. Bruk denne informasjonen til å finne punktet på grafen for hver linje, når x = 1. (Alternativt, bytt ut x = 1 for enhver ligning og løs for y).

I vårt eksempel er regelen y = -2x + 5 en skråning av -2. Ved x = 1 faller linjen 2 nedfra punktet x = 0. Tegn linjestykket mellom (0,5) og (1,3).

Regelen y = ½x + 0har en helning på ½. Ved x = 1 går linjen ½ opp fra punktet x = 0. Tegn linjestykket mellom (0,0) og (1,½).

Hvis linjene har samme helning linjene vil aldri krysse hverandre, så det er ingen løsning for ligningssystemet. Skrive: ingen løsning.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 18

6. Fortsett å tegne linjene til de krysser hverandre. Stopp og se på diagrammet ditt. Hvis linjene allerede har krysset hverandre, fortsett til neste trinn. Ellers tar du en avgjørelse basert på hva linjene gjør:

Hvis linjene beveger seg mot hverandre, vil du fortsette å tegne punkter i den retningen.

Hvis linjene beveger seg bort fra hverandre, gå tilbake og tegne punkter i den andre retningen, med start på x = -1.

Hvis linjene ikke er i nærheten av hverandre, hopper du videre og plotter fjernere punkter, for eksempel x = 10.

Bilde med tittelen Solve Systems of Algebraic Equations Containing Two Variables Trinn 19

7. Finn svaret i skjæringspunktet mellom linjene. Når de to linjene krysser hverandre, er x- og y-verdiene på det punktet løsningen på problemet. Hvis du er heldig, vil svaret være et heltall. For eksempel, i våre eksempler, krysser de to linjene (2.1) så er svaret ditt x = 2 og y = 1. I noen ligningssystemer vil linjene krysse hverandre med en verdi mellom to heltall, og med mindre grafen din er ekstremt nøyaktig, vil det være vanskelig å si hvor dette er. Hvis dette er tilfelle, kan du gi et svar som: `x er mellom 1 og 2`. Du kan også bruke substitusjonsmetoden eller elimineringsmetoden for å finne det nøyaktige svaret.

Tips

Du kan sjekke arbeidet ditt ved å mate svarene tilbake til de opprinnelige ligningene. Hvis ligningene er sanne (for eksempel 3 = 3), er svaret ditt riktig.
I eliminasjonsmetoden må du noen ganger multiplisere en ligning med et negativt tall for å eliminere en variabel.

Advarsler

Disse metodene kan ikke brukes når du arbeider med et potenstall, for eksempel x. For mer informasjon om ligninger av denne typen trenger du en veiledning for faktorisering av kvadrater med to variabler.