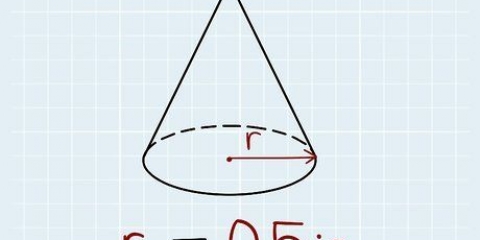
I eksemplet er sidene av bunnen av pyramiden alle 5 cm, og du beregner arealet av bunnen som følger: 
Husk at todimensjonale områder uttrykkes i kvadrater – kvadratcentimeter, meter, kilometer, etc. 
I eksemplet antar vi at pyramiden har en høyde på 9 cm. I dette tilfellet multipliserer du arealet av basen med denne verdien, som følger: 
Husk at volumer er uttrykt i kubikkenheter. I dette tilfellet, fordi alle lineære mål er centimeter, er volumet angitt i kubikkcentimeter. 
I eksemplet deler du 225 cm med 3 og svaret er 75 cm for volumet. 


Denne erstatningen ser slik ut: 


 .....(opprinnelig ligning)
.....(opprinnelig ligning) .....(kvadrat på begge sider)
.....(kvadrat på begge sider) .....(skriv inn verdier)
.....(skriv inn verdier) .....(forenkle brøk)
.....(forenkle brøk) .....(forenkle firkantet)
.....(forenkle firkantet) .....(trekke fra)
.....(trekke fra) .....(forenkle root)
.....(forenkle root)
Fra beregningene trekker vi ut at høyden på pyramiden er 12 cm. Bruk dette sammen med 10 cm-siden av basen for å beregne volumet til pyramiden: 









 ..........(justert ligning)
..........(justert ligning) ..........(bytt ut h på begge sider)
..........(bytt ut h på begge sider) ..........(trekk fra kvadratroten av begge sider)
..........(trekk fra kvadratroten av begge sider) ..........(fyll inn tallene)
..........(fyll inn tallene) ..........(forenkle rutene)
..........(forenkle rutene) ..........(trekk fra verdier)
..........(trekk fra verdier) ..........(forenkle kvadratroten)
..........(forenkle kvadratroten)Doble denne verdien for å finne diagonalen til den kvadratiske bunnen av pyramiden. Dermed er diagonalen til bunnen av pyramiden 9,8 * 2 = 19,6 cm. 
I dette pyramideeksemplet er diagonalen til basen 19,6 cm. Derfor er siden lik: 





Beregne volumet til en firkantet pyramide
Innhold
En firkantet pyramide er en tredimensjonal figur med en firkantet base og trekantede skråninger som møtes på ett punkt over basen. I tilfelle det 


Trinn
Metode 1 av 3: Bestem volumet med arealet av basen og høyden

1. Mål lengden på siden av basen. Siden firkantede pyramider per definisjon har en firkantet base, bør alle sider av basen ha lik lengde. Så med en firkantet pyramide trenger du bare å vite lengden på en av sidene.
- Anta at du har en pyramide med en firkantet base hvis sider har en lengde på
. Du vil bruke denne verdien til å beregne arealet av basen.
- Hvis sidene av basen ikke er like lange, har du en rektangulær pyramide i stedet for en firkantet pyramide. Formelen for volumet til en rektangulær pyramide er veldig lik formelen for kvadratiske pyramider. I tilfelle det
er lengden på bunnen av den rektangulære pyramiden og
bredden, deretter volumet til pyramiden
.

2. Beregn arealet av basen. For å bestemme volumet trenger du først arealet av basen. Dette gjør du ved å multiplisere lengden og bredden på basen. Siden bunnen av en firkantet pyramide er en firkant, har alle sidene samme lengde, og arealet av bunnen er lik kvadratet på lengden på en av sidene (dermed multiplisert med seg selv).


3. Multipliser arealet av basen med høyden på pyramiden. Deretter multipliserer du grunnflaten med høyden på pyramiden. Som en påminnelse er høyden avstanden er lengden på linjestykket fra toppen av pyramiden til basen, i rette vinkler.


4. Del dette svaret med 3. Til slutt bestemmer du volumet til pyramiden ved å dele verdien du nettopp fant (ved å multiplisere arealet av basen med høyden) med 3. Dette beregner volumet av den firkantede pyramiden.
Metode 2 av 3: Bestem volumet med apotemet

1. Mål apotemet til pyramiden. Noen ganger er den vinkelrette høyden til pyramiden ikke gitt (eller du må måle den), men apotemet. Med apotemet kan du bruke Pythagoras teorem brukes til å beregne vinkelrett høyde.
- Apotemet til en pyramide er avstanden fra toppen til midten av en av sidene av basen. Mål til midten av en av sidene og ikke til et av hjørnene på basen. For dette eksemplet antar vi at apotem er 13 cm og lengden på den ene siden av basen er 10 cm.
- Husk at Pythagoras teorem kan uttrykkes som ligningen
, hvorved
og
de vinkelrette bena er av den rette trekanten og
hypotenusen.

2. Se for deg en rettvinklet trekant. For å bruke Pythagoras teorem trenger du en rettvinklet trekant. Se for deg en trekant som deler pyramiden i to og vinkelrett på bunnen av pyramiden. Pyramidens apotem, kalt  , er hypotenusen til denne rette trekanten. Basen til denne rettvinklet er halvparten av lengden av
, er hypotenusen til denne rette trekanten. Basen til denne rettvinklet er halvparten av lengden av  , siden av den firkantede bunnen av pyramiden.
, siden av den firkantede bunnen av pyramiden.
 , er hypotenusen til denne rette trekanten. Basen til denne rettvinklet er halvparten av lengden av
, er hypotenusen til denne rette trekanten. Basen til denne rettvinklet er halvparten av lengden av  , siden av den firkantede bunnen av pyramiden.
, siden av den firkantede bunnen av pyramiden.
3. Tilordne variabler til verdiene. Pythagoras teorem bruker variablene a, b og c, men det er nyttig å erstatte dem med variabler som er meningsfulle for problemet ditt. apotemet  tar plassen til
tar plassen til  i Pythagoras teorem. Benet til den rette trekanten (
i Pythagoras teorem. Benet til den rette trekanten ( ), tar plassen til
), tar plassen til  Du går høyden
Du går høyden  bestemme pyramiden, som opptar plassen til
bestemme pyramiden, som opptar plassen til  i Pythagoras teorem.
i Pythagoras teorem.
 tar plassen til
tar plassen til  i Pythagoras teorem. Benet til den rette trekanten (
i Pythagoras teorem. Benet til den rette trekanten ( ), tar plassen til
), tar plassen til  Du går høyden
Du går høyden  bestemme pyramiden, som opptar plassen til
bestemme pyramiden, som opptar plassen til  i Pythagoras teorem.
i Pythagoras teorem.


4. Bruk Pythagoras teorem til å beregne den vinkelrette høyden. Bruk de målte verdiene  og
og  . Løs deretter ligningen:
. Løs deretter ligningen:
 og
og  . Løs deretter ligningen:
. Løs deretter ligningen: .....(opprinnelig ligning)
.....(opprinnelig ligning) .....(kvadrat på begge sider)
.....(kvadrat på begge sider) .....(skriv inn verdier)
.....(skriv inn verdier) .....(forenkle brøk)
.....(forenkle brøk) .....(forenkle firkantet)
.....(forenkle firkantet) .....(trekke fra)
.....(trekke fra) .....(forenkle root)
.....(forenkle root)
5. Bruk høyde og base for å beregne volum. Etter å ha brukt disse beregningene på Pythagoras teorem har du nå informasjonen du trenger for å beregne volumet av pyramiden. Bruk formelen  og løs disse, pass på å gi svaret i kvadratiske enheter.
og løs disse, pass på å gi svaret i kvadratiske enheter.
 og løs disse, pass på å gi svaret i kvadratiske enheter.
og løs disse, pass på å gi svaret i kvadratiske enheter.



Metode 3 av 3: Bestemme volumet med høyden på bena

1. Mål høyden på bena til pyramiden. Høyden på bena er lengden på kantene på pyramiden, målt fra toppen til et av hjørnene på basen. Som ovenfor, bruk Pythagoras teorem for å beregne den vinkelrette høyden til pyramiden.
- I dette eksemplet antar vi at høyden på bena er 11 cm og at den vinkelrette høyden er 5 cm.

2. Se for deg en rettvinklet trekant. Igjen trenger du en rettvinklet trekant for å kunne bruke Pythagoras teorem. I dette tilfellet er imidlertid den ukjente verdien bunnen av pyramiden. Kjent er den vertikale høyden og høyden på bena. Forestill deg nå å kutte pyramiden diagonalt fra det ene hjørnet til det andre, og deretter åpne figuren, det resulterende planet vil se ut som en trekant. Høyden på trekanten er den vinkelrette høyden til pyramiden. Dette deler den eksponerte trekanten i to symmetriske rette trekanter. Hypotenusen til hver av de rette trekantene er høyden på pyramidens ben. Grunnlaget til hver av de rette trekantene er halvparten av diagonalen til bunnen av pyramiden.

3. Tilordne variabler. Bruk den imaginære rettvinklede trekanten og tilordne verdier til Pythagoras teorem. Du vet den vertikale høyden,  som er den ene siden av Pythagoras teorem,
som er den ene siden av Pythagoras teorem,  . Høyden på bena til pyramiden,
. Høyden på bena til pyramiden,  danner hypotenusen til denne imaginære rettvinklede trekanten, og tar derfor plassen til
danner hypotenusen til denne imaginære rettvinklede trekanten, og tar derfor plassen til  . Den ukjente diagonalen til bunnen av pyramiden er den gjenværende siden av den rette trekanten,
. Den ukjente diagonalen til bunnen av pyramiden er den gjenværende siden av den rette trekanten,  Etter å ha gjort disse erstatningene, ser ligningen slik ut:
Etter å ha gjort disse erstatningene, ser ligningen slik ut:
 som er den ene siden av Pythagoras teorem,
som er den ene siden av Pythagoras teorem,  . Høyden på bena til pyramiden,
. Høyden på bena til pyramiden,  danner hypotenusen til denne imaginære rettvinklede trekanten, og tar derfor plassen til
danner hypotenusen til denne imaginære rettvinklede trekanten, og tar derfor plassen til  . Den ukjente diagonalen til bunnen av pyramiden er den gjenværende siden av den rette trekanten,
. Den ukjente diagonalen til bunnen av pyramiden er den gjenværende siden av den rette trekanten,  Etter å ha gjort disse erstatningene, ser ligningen slik ut:
Etter å ha gjort disse erstatningene, ser ligningen slik ut:


4. Regn ut diagonalen til kvadratbasen. Du må omorganisere ligningen for å få variabelen  isolere, og beregne deretter verdien.
isolere, og beregne deretter verdien.
 isolere, og beregne deretter verdien.
isolere, og beregne deretter verdien. ..........(justert ligning)
..........(justert ligning) ..........(bytt ut h på begge sider)
..........(bytt ut h på begge sider) ..........(trekk fra kvadratroten av begge sider)
..........(trekk fra kvadratroten av begge sider) ..........(fyll inn tallene)
..........(fyll inn tallene) ..........(forenkle rutene)
..........(forenkle rutene) ..........(trekk fra verdier)
..........(trekk fra verdier) ..........(forenkle kvadratroten)
..........(forenkle kvadratroten)
5. Finn siden av bunnen av diagonalen. Basen på pyramiden er en firkant. Diagonalen til hver kvadrat er lik lengden på en av sidene, ganger kvadratroten 2. Og så kan du finne siden av et kvadrat ved å dele diagonalen med kvadratroten 2.


6. Beregn volumet ved å bruke siden og høyden. Gå tilbake til den opprinnelige formelen for å beregne volum ved å bruke side og vinkelrett høyde.




Tips
- I en firkantet pyramide kan den vinkelrette høyden, apotem og lengden på kanten av basen alle beregnes ved å bruke Pythagoras teorem.
Artikler om emnet "Beregne volumet til en firkantet pyramide"
Оцените, пожалуйста статью
Lignende
Populær