Hvordan beregne volumet til en pyramide: 8 trinn (med bilder)

Innhold

Trinn
- Metode 1 av 2: Pyramide med rektangulær base
- Metode 2 av 2: Pyramide med en trekantet base
Tips
Advarsler

For å beregne volumet til en pyramide, multipliser arealet av basen med høyden på pyramiden. Del resultatet med 3, det er alt! Les denne artikkelen med beregningsmetoder for en pyramide med rektangulær base og en pyramide med trekantet base.

Trinn

Metode 1 av 2: Pyramide med rektangulær base

1. Bestem lengden og bredden på basen. I dette eksemplet er lengden 4 cm og bredden 3 cm. Hvis du har en firkantet base, er metoden den samme, bare lengden og bredden er like. Skriv ned målene dine.

Bilde med tittelen Beregn volumet til en pyramide Trinn 2

2. Multipliser lengden med bredden for å beregne arealet av basen. For å beregne arealet til eksemplet vårt, multipliserer vi 3 cm med 4 cm. 3cm x 4cm = 12cm

Bilde med tittelen Beregn volumet til en pyramide Trinn 3

3. Multipliser arealet av basen med høyden. Arealet av basen er 12 cm og høyden er 4 cm, så vi multipliserer 12 cm med 4 cm. 12cm x 4cm = 48cm

Bilde med tittelen Beregn volumet til en pyramide Trinn 4

4. Del resultatet med 3. Det er det samme som å multiplisere med 1/3. 48cm/3 = 16cm. Volumet av en pyramide med en høyde på 4 cm og en rektangulær base med en bredde på 3 cm og en lengde på 4 cm er derfor 16 cm. Ikke glem å angi utfallet i kubikkenheter.

Metode 2 av 2: Pyramide med en trekantet base

Bilde med tittelen Beregn volumet til en pyramide Trinn 5

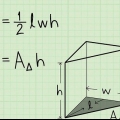
1. Bestem lengden og bredden på basen. Lengden og bredden på basen må vinkelrett på hverandre, ellers vil ikke denne metoden fungere. De kan også sees som bunnen og høyden på trekanten. I dette eksemplet er trekantens bredde 2 cm og lengden 4 cm. Skriv ned dette.

Bilde med tittelen Beregn volumet til en pyramide Trinn 6

2. Beregn arealet av basen. For å beregne arealet av basen bruker vi følgende formel:A = 1/2(o)(h). Dette er hvordan vi gjør det:

A = 1/2(o)(h)

A = 1/2(2)(4)

A = 1/2(8)

A = 4 cm

Bilde med tittelen Beregn volumet til en pyramide Trinn 7

3. Multipliser arealet av basen med høyden på pyramiden. Arealet av basen er 4 cm og høyden er 5 cm. 4cm x 5cm = 20cm.

Bilde med tittelen Beregn volumet til en pyramide Trinn 8

4. Del resultatet med 3. 20cm/3 = 6,67cm. Volumet til en pyramide med en høyde på 5 cm og en trekantet base med en bredde på 2 cm og en lengde på 4 cm er derfor 6,67 cm.

Tips

I en pyramide med kvadratisk base er høyden, linjen som deler den trekantede siden i to like trekanter og bredden på basen forbundet med Pythagoras teorem: (bredde ÷ 2) + (høyde) = (trekantens høyde)
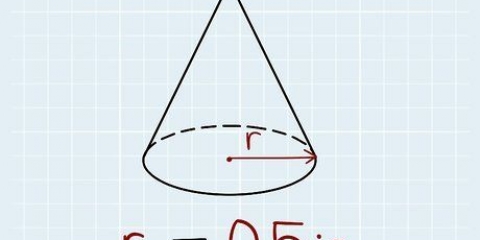
Denne metoden kan også brukes på objekter som femkantede pyramider, sekskantede pyramider, etc. Den generelle prosessen er: A) beregne arealet av basen; B) mål høyden fra toppen av pyramiden til midten av basen; C) multipliser A med B; D) del på 3.
I alt vanlig pyramidene er de oppreiste ribbeina, linjen som deler den trekantede siden i to like trekanter og bredden på basen forbundet med Pythagoras teorem: (lengde på siden ÷ 2) + (lengde på ribben) = (høyde)

Advarsler

Pyramider har tre typer høyder: linjen som deler den trekantede flaten i to like trekanter, lengden på ribben (langs siden av en trekantet flate), og den faktiske høyden (fra spissen av pyramiden vinkelrett ned til basen) . ).